Всем доброго времени суток! В прошлой статье я рассказывал о дросселе и его параметрах. В частности рассмотрел межвитковую ёмкость и индуктивность рассеивания обмоток. Данные параметры влияют на реактивную мощность дросселя, кроме потерь реактивной мощности в дросселе присутствуют параметры, вызывающие потери активной мощности. Это во-первых, сопротивление обмоточного провода дросселя и активные потери в сердечнике. Данная статья посвящена активным потерям в обмотках дросселя.
Для сборки радиоэлектронного устройства можно преобрески DIY KIT набор по ссылке.
Потери мощности в дросселе
Рассматривая эквивалентную схему замещения дросселя, было показано, что дроссель содержит активное сопротивление обмоток R, а также проводимость gμ. Данные параметры потребляют активную мощность, которая в первую очередь выделяется в качестве тепла, то есть дроссель нагревается. Температура нагрева в первую очередь определяет расчётные параметры дросселя. Мощность, которая приводит к выделению активной мощности, называется потерями мощности. Данные потери состоят из двух частей: потери мощности на протекание тока через активное сопротивление обмоток ∆P1 и потери мощности на перемагничивание и вихревые токи в сердечнике ∆P2
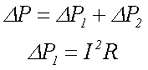
где ∆P – суммарные потери мощности,
∆P1 – потери мощности в обмотках дросселя,
∆P2 – потери мощности в сердечнике,
I – действующее значение тока, протекающего в дросселе,
R – активное сопротивление обмоток,
Значение тока I в дросселе зависит от формы напряжения и его амплитудного значения. Потери мощности в сердечнике ∆P2, зависят от материала сердечника и его размеров, а также от характеристик напряжения и тока.
Влияние напряжения и тока на потери мощности в дросселе
Как известно электрическая мощность на участке цепи определяется произведением мгновенных значений напряжения u и электрического тока i на этом участке
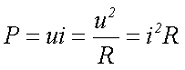
где R – сопротивление участка цепи.
Однако на практике неудобно пользоваться параметрами мгновенных значений, поэтому чаще всего оперируют величинами действующих значений напряжения U и тока I или средними значениями напряжения Ucp и тока Icp. Действующее значение характеризует тепловое действие переменного тока и напряжения, а среднее значение является среднеарифметическим значением всех амплитудных значений переменного напряжения за некоторый промежуток времени.
В радиоэлектронных приборах и устройствах используются различные типы переменных напряжений и токов, которые, кроме значений напряжений токов, характеризуются безразмерными параметрами: коэффициентом формы kф и коэффициентом амплитуды kа. Коэффициент амплитуды, как относятся между собой значения действующих значений к средним значениям, а коэффициент амплитуды – отношение амплитудного значения к действующему значению
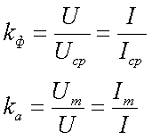
Данные параметры характеризует форму переменного напряжения и тока. Рассмотрим некоторые типы форм напряжения.
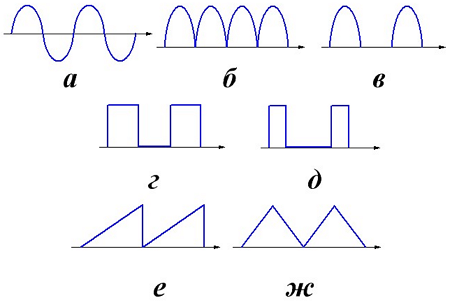
Некоторые формы напряжения и тока.
На рисунке изображено синусоидальное напряжение а, после двухполупериодного выпрямителя б, после однополупериодного выпрямителя в, прямоугольная форма (меандр, коэффициент заполнения D = 0,5) г, последовательность импульсов (коэффициент заполнения D ≠ 0,5) д, пилообразная форма е, треугольная форма ж. Для данных форм напряжения коэффициенты формы и амплитуды будут иметь значение
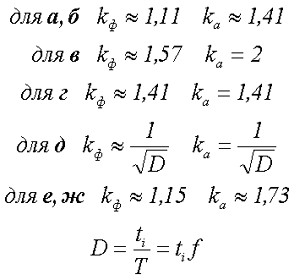
где D – коэффициент заполнения, равный отношению длительности импульса к его периоду,
ti – длительность импульса,
T – период следования импульсов,
f – частота следования импульсов.
Как видно из данных выражений, по известной форме переменного напряжения или тока достаточно просто определить активную мощность потребляемую нагрузкой, кроме того в случае прямоугольной формы напряжения изменяя длительность импульса можно регулировать действующее напряжение и электрический ток. Теперь разберёмся с сопротивлением дросселя и мощностью потерь в сердечнике.
Как определить сопротивление обмоток дросселя?
Сопротивление обмотки дросселя R определяется длинной провода катушки, зависящей от размеров сердечника, количества витков провода и удельного сопротивления проводника
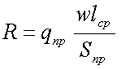
где w – количество витков провода,
lcp – средняя длина витка провода,
Sпр – площадь поперечного сечения провода,
qпр – удельное электрическое сопротивление вещества провода.
Для определения средней длины витка в случае цилиндрического сердечника можно по следующей формуле
![]()
где Dc – диаметр каркаса, на который наматывается обмотка дросселя или, в случае бескаркасной намотки – диаметр сердечника,
m – число слоёв намотки,
dи – диаметр провода с изоляцией. Отмечу, что маркировка провода и идет без учёта изоляции, обычно толщина изоляции составляет 0,03…0,1 мм.
В случае прямоугольного сердечника или каркаса средняя длина витка в обмотке составляет
![]()
где а, b – стороны прямоугольника образующего сечение сердечника дросселя,
m – число слоёв намотки,
dи – диаметр провода с изоляцией.
В случае, если необходимо учесть изменение сопротивления провода из-за изменения температуры, необходимо внести поправку на повышение температуры
![]()
где R20 – сопротивление провода при температуре 20 °С (стандартная температура, при которой нормируется удельное сопротивление веществ), считается по вышеизложенной формуле,
α – температурный коэффициент сопротивления,
Т – температура до которой нагрелся проводник,
20 – стандартная температура, при которой нормируется удельное сопротивление веществ.
Данные выражения позволяют вычислить сопротивление обмотки дросселя при постоянном токе или токе низкой частоты, однако уже на частотах выше 1 кГц активное сопротивление начинает заметно расти, вследствие поверхностного эффекта (скин-эффект) и влияния соседних проводников обмотки (эффект близости). Для учёта роста сопротивления ввели добавочный коэффициент kд, который показывает во сколько раз сопротивление на данной частоте больше, чем сопротивление при постоянном токе. Тогда сопротивление обмоток дросселя на заданной частоте вычисляется по следующему выражению
![]()
где RПТ – сопротивление обмотки дросселя при постоянном токе,
kд – коэффициент добавочных потерь.
Коэффициент добавочных потерь зависит от глубины скин-слоя и количества слоёв дросселя. Глубина скин-слоя определяется следующим выражение
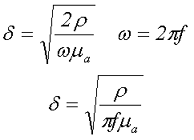
где f – частота переменного тока,
μа – абсолютная магнитная проницаемость вещества проводника,
ρ – удельное электрическое сопротивление.
Таким образом, в одиночном проводнике ток на высокой частоте протекает по внешней части проводника. Однако в катушке близко лежащие витки вытесняют ток на внешнюю часть обмотки, и в этом случае сопротивление проводника ещё больше увеличивается и зависит от количества слоев в обмотке дросселя, причём с ростом числа слоёв сопротивление первого слоя возрастает.
Для определения коэффициента добавочных потерь на сопротивление обмоток дросселя можно воспользоваться следующей формулой
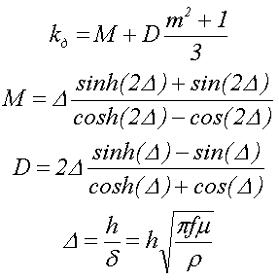
где δ – глубина скин-слоя,
h – высота одного слоя,
m – количество слоёв в обмотке дросселя,
sinh и cosh – гиперболические синус и косинус.
Гиперболические функции могут быть преобразованы к следующему виду
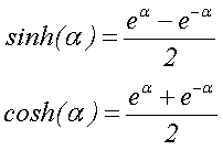
В выражении для вычисления коэффициента добавочных потерь, значение высоты одного слоя соответствует квадратным проводникам расположенным «виток к витку», однако в большинстве случаев провод из которого мотается дроссель круглого сечения или состоит из нескольких свитых вместе проводников – литцендрата. Таким образом, необходимо диаметр проводника преобразовать к эквивалентной высоте слоя hэ
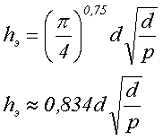
где d – диаметр проводника,
p – расстояние между центрами проводников.
В случае использования многожильного провода (литцендрата), выражение для коэффициента добавочных потерь будет иметь вид
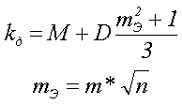
где mэ – эквивалентное количество слоёв,
n – количество жил в многожильном проводе (литцендрат).
Необходимо отметить, что использование провода определённого диаметра или многожильного провода необходимо оценивать в ходе проверочных расчётов. А в общем случае необходимо снижать количество слоёв обмотки дросселя.
Пример расчёта потери мощности в обмотке дросселя
Рассчитаем активные потери в обмотке дросселя, состоящего из 40 витков w = 40 круглого провода диаметром по меди dп = 1 мм, диаметр провода с изоляцией dи = 1,07 мм при протекании переменного электрического тока прямоугольной формы с амплитудой Im = 5 A, частота f = 50 кГц, коэффициент заполнения D = 0,5, провод намотан на круглый сердечник диаметром DC = 10 мм в 4 слоя m = 4. Температура работы дросселя T = 85 °С. Удельное электрическое сопротивление меди qCu = 0,0171, температурный коэффициент сопротивления αCu = 0,0038.
Определим сопротивление катушки при постоянном токе, для чего вычислим среднюю длину витка
![]()
Тогда сопротивление катушки составит
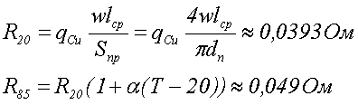
где R20 – сопротивление при температуре 20 °C,
R85 – сопротивление при температуре 85 °C.
Определим коэффициент дополнительных потерь kд обмоток дросселя на частоте 50 кГц
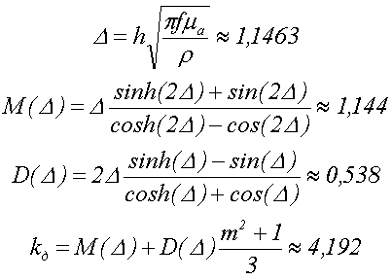
Тогда сопротивление обмоток дросселя и мощность потерь составит
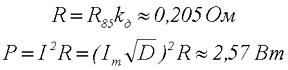
Если же использовать литцендрат такого же диаметра, например ЛЕП 49х0,1, состоящий из 49 жилок диаметром 0,1 мм и имеющий суммарную площадь поперечного сечения Sпр = 0,385 мм2, а диаметр провода 1,12 мм, тогда
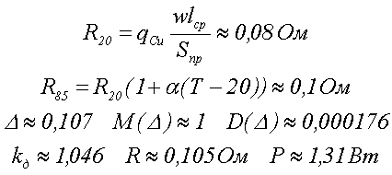
Как видно, при использовании литцендрата увеличивается сопротивление при постоянном токе, однако на высоких частотах за счёт скин-эффекта и поверхностного эффекта, литцендрат имеет преимущество перед сплошным проводом.
Теория это хорошо, но необходимо отрабатывать это всё практически ПОПРОБОВАТЬ МОЖНО ЗДЕСЬ
 Тепловой режим трансформатора. Часть 2
Тепловой режим трансформатора. Часть 2 Расчёт трансформатора — 1. Выбор сердечника.
Расчёт трансформатора — 1. Выбор сердечника.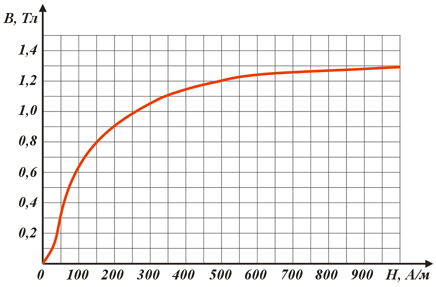 Пример расчёта сердечника трансформатора
Пример расчёта сердечника трансформатора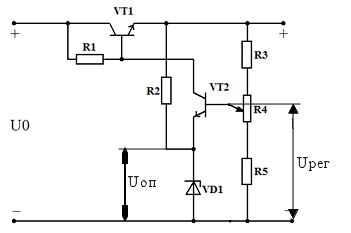 Компенсационные стабилизаторы напряжения.
Компенсационные стабилизаторы напряжения.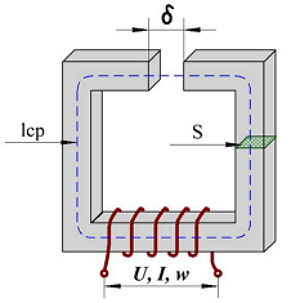 Катушки индуктивности с малым воздушным зазором
Катушки индуктивности с малым воздушным зазором