Всем доброго времени суток! В прошлой статье я рассказал о дросселях сглаживающих фильтров и изложил принцип их расчёта. Однако такие типы дросселей в бытовой технике применяются не очень часто, так как в маломощных устройствах зачастую эффективнее использовать ёмкостные фильтры. Наиболее часто в электронных устройствах применяют другой вид дросселей – дроссели переменного тока. Об их особенностях, принципах работы и расчёте параметров таких дросселей пойдёт речь в этой статье.

Для сборки радиоэлектронного устройства можно преобрески DIY KIT набор по ссылке.

Особенности работы дросселя переменного тока

Дроссель переменного тока, так же как и любой другой дроссель представляет собой катушку индуктивности с ферромагнитным сердечником. Данный тип дросселя включается последовательно с нагрузкой, аналогично сглаживающему дросселю, но в отличие от него, протекающий ток через дроссель переменного тока не имеет постоянного тока подмагничивания. В связи с этим дроссель переменного тока широко применяется в балластных и токоограничительных цепях, мощных антенных и фильтрующих устройствах, а так же в различных импульсных преобразователях напряжения.

В независимости от применения дросселя в схеме его работа основана на зависимости его реактивного сопротивления X_L от частоты f протекающего через него тока I_H и падении напряжения на дросселе U_L

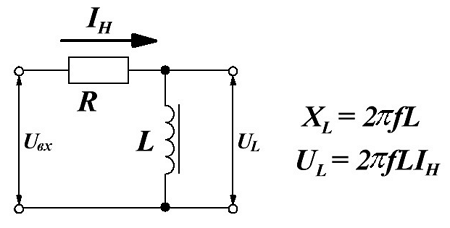
Дроссель переменного тока.

Таким образом, величина напряжения на дросселе U_L определяется индуктивностью дросселя L и параметрами тока, протекающего через дроссель: частота тока f и значение тока в цепи I_H.

Влияние немагнитного зазора на дроссель

В предыдущих статьях я рассказывал о негативном влиянии насыщения сердечника на снижение магнитной проницаемости μ_e и индуктивности дросселя L, которые приводят к искажению формы тока протекающего через дроссель.

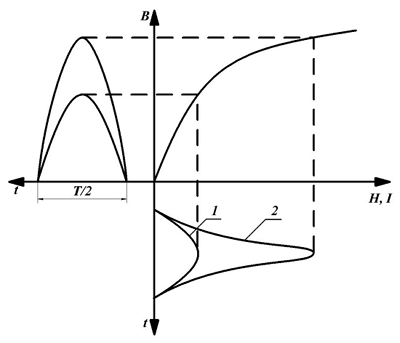
Форма тока, протекающего через дроссель: для ненасыщенного сердечника (1) и для насыщенного сердечника (2).

На данном рисунке изображено искажение формы тока синусоидального напряжения при работе дросселя на насыщенном и ненасыщенном участке кривой намагничивания. Степень искажения формы напряжения зависит также от отношения реактивного сопротивления дросселя к активному сопротивлению нагрузки X_L/R_H. То есть при насыщении сердечника, чем меньше данное соотношение, тем меньше степень искажения формы напряжения. Таким образом, введение немагнитного зазора кроме стабилизации величины индуктивности, в широких пределах изменения тока, позволяет пропустить через дроссель переменный ток без значительных изменений.

Кроме вышеописанных факторов, введение немагнитного зазора приводит к некоторым особенностям, которые необходимо учитывать при разработке и изготовлении дросселей с зазором. Основной особенностью является уширение магнитного потока в зазоре.

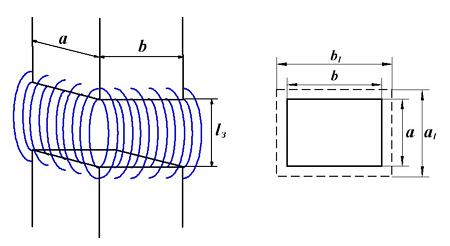
Уширение магнитного потока в немагнитном зазоре дросселя: стержень дросселя (слева) и его поперечное сечение (справа). Пунктиром обозначены размеры увеличенного сечения вследствие выпучивания магнитного потока.

Данное явление связанно с тем, что в дросселе с зазором магнитный поток выходит за пределы пространства, находящегося между двух концов разрезанного сердечника, поэтому площадь поперечного сечения в немагнитном зазоре как бы увеличивается.

Размеры уширения сечения зависит от длины обмотки дросселя l_об, площади сечения сердечника S_e и длины немагнитного зазора l_з. Уширение магнитного потока уменьшает магнитное сопротивление цепи и, следовательно, увеличивает индуктивность дросселя. Для учёта уширения магнитного потока и увеличения индуктивности вводится коэффициент выпучивания F, учитывающий уширение магнитного потока в немагнитном зазоре. Поэтому значение индуктивности дросселя будет определятся следующим выражением

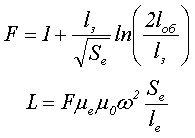
где ω – количество витков провода в обмотке,

μ₀ – магнитная постоянная, μ₀ = 4π*10^-7 Гн/м,

μ_е – эквивалентная (относительная) магнитная проницаемость сердечника,

S_е – эквивалентная площадь поперечного сечения сердечника,

l_е – эквивалентная длина магнитной линии сердечника.

l_M – длина магнитной линии в сердечнике.

F – коэффициент, учитывающий уширение магнитного потока в зазоре.

Принципы расчёта дросселей переменного тока

Расчёт дросселя переменного тока ведётся аналогично расчёту сглаживающего дросселя, но с учётом начальных условий. Так для дросселя переменного тока определяющими параметрами являются: требуемая индуктивность L, приложенное напряжение U_L, частота переменного тока f, перегрев дросселя. Кроме этого необходимо определиться с материалом сердечника дросселя, который определят индукцию насыщения B_S и максимальную индукцию в сердечнике B_m, которая для предотвращения насыщения сердечника выбирается из условия

В основе расчётов дросселя переменного тока лежит выражения для определения величина действующего напряжения падающего на дросселе U_L

где f – частота переменного тока,

L – индуктивность дросселя,

I – действующее значение тока дросселя.

Тогда с учетом выражения для индуктивности дросселя с замкнутым сердечником и выражения для максимальной индукции в сердечнике напряжение на дросселе будет зависеть от следующих параметров

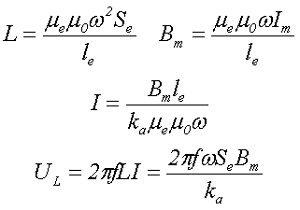
где μ_е – эквивалентная магнитная проницаемость сердечника,

μ₀ – магнитная постоянная, μ₀ = 4π•10^-7 Гн/м,

ω – количество витков обмотки дросселя,

S_e – эквивалентное сечение сердечника дросселя,

l_e – эквивалентная длина магнитного пути сердечника дросселя,

B_m – максимальное значение магнитной индукции сердечника,

k_a – коэффициент амплитуды тока (напряжения) дросселя.

Получившееся выражение довольно часто можно встретить под названием основной формулы трансформаторной ЭДС, так как оно устанавливает однозначное соотношение, между ЭДС на зажимах обмотки и числом витков обмотки, при заданной величине магнитной индукции в сердечнике. Тогда при синусоидальном напряжении (коэффициент амплитуды k_a ≈ 1,414) выражение принимает следующий вид

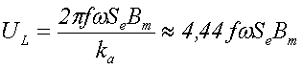
Вернёмся к исходному выражению для напряжения на дросселе U_L, в котором неоднозначным является параметр – количество витков. Данный параметр кроме всего прочего (величины индуктивности L и магнитной проницаемости μ_е сердечника) зависит от размеров магнитопровода, а конкретнее от площади окна S_O, которое можно вычислить по следующему выражению

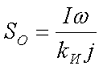
где I – действующее значение тока дросселя,

ω – количество витков обмотки дросселя,

k_И – коэффициент использования окна сердечника,

j – плотность тока в проводе обмотки.

Параметры k_И и j выбирают аналогично, как и для дросселя сглаживающего фильтра, то есть коэффициент использования окна сердечника k_И ≈ 0,3, а плотность тока j = 5 А/мм².

Тогда выражая из данного выражения количество витков провода ω, получим

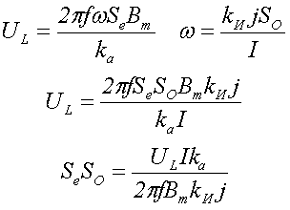
Получившееся выражение определяет основное расчётное выражение для определения типоразмера сердечника – произведение площадей сердечника S_eS_O. После преобразования выражения для действующего напряжения на дросселе U_L определяем количество витков обмотки ω и величину немагнитного зазора δ

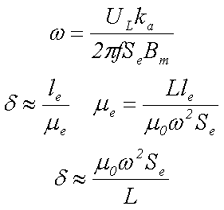
где μ_е – эквивалентная магнитная проницаемость сердечника,

μ₀ – магнитная постоянная, μ₀ = 4π•10^-7 Гн/м,

S_e – эквивалентное сечение сердечника дросселя,

l_e – эквивалентная длина магнитного пути сердечника дросселя,

B_m – максимальное значение магнитной индукции сердечника,

k_a – коэффициент амплитуды тока (напряжения) дросселя.

Вычисленное количество витков является ориентировочным, так как из-за уширения магнитного потока значение индуктивности оказывается несколько больше при данном количестве витков, что в некоторых случаях является нежелательным. Поэтому необходимо пересчитать витки с учётом коэффициента уширения магнитного потока F

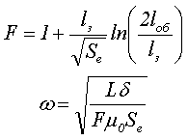
Осталось выбрать сечение обмоточного провода S_П

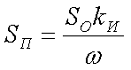
где S_O – площадь окна используемого сердечника,

k_И – коэффициент использования окна сердечника,

ω – количество витков обмотки дросселя.

Выбор сечения провода необходимо производить, округлив полученное значение до ближайшего номинала, при этом необходимо учитывать, что на высоких частотах возрастают потери мощности в проводе. Поэтому при достаточно высокой частоте необходимо использовать обмоточный провод, состоящий из нескольких жил, при этом диаметр жилы выбирают исходя из глубины скин-слоя δ

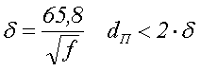
где f – частота переменного тока, протекающего через дроссель,

δ – толщина скин-слоя,

d_п – диаметр жилы в обмоточном проводе.

После конструктивного расчёта сердечника и обмотки необходимо проверить тепловой режим работы дросселя – нагрев и перегрев дросселя.

Расчёт дросселя переменного тока

В качестве примера рассчитаем дроссель переменного тока со следующими исходными данными: индуктивность дросселя L = 20 мкГн, частота переменного тока f = 50 кГц, действующее значение тока дросселя I_д = 5 А, температура перегрева ∆Т = 50 °C. Ток, протекающий через дроссель, имеет форму прямоугольных импульсов с коэффициентом заполнения D = 0,5.

В общем случае расчёт сводится к выбору параметров магнитопровода и обмотки, при этом режим работы дросселя должен отвечать заданным условиям, в данном случае, температуре перегрева ∆Т.

1.Выберем типоразмер сердечника соответствующего произведению площадей S_eS_O. Для этого необходимо дополнительно определить действующее напряжение на дросселе U_L, коэффициент амплитуды тока дросселя k_a, коэффициент использования окна сердечника k_И, значение максимальной индукции тока дросселя B_m и плотность тока j.

Так как частота тока достаточно высокая, то в качестве материала магнитопровода выберем феррит марки N87, следовательно, B_m = 0,3. Коэффициент использования окна сердечника и плотность тока выберем соответственно k_И = 0,3 и j = 5 А/мм².

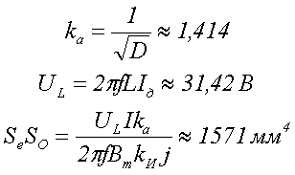
Таким образом, выберем магнитопровод, состоящий из двух половинок типа E 20/10/6 со следующими параметрами: l_e = 93мм, S_e = 32 мм², S_O = 57 мм², V_e = 2980 мм³, S_eS_O = 1824 мм⁴.

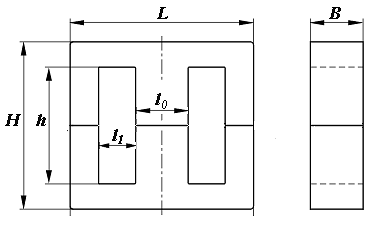
Сердечник, состоящий из двух половинок Е 20/10/6, имеет следующие размеры:

L = 20,4 мм, H = 20,2 мм, B = 5,9 мм, h = 14 мм, l₀ = 5,9 мм, l₁ = 4,1 мм.

2.Определим предварительное число витков обмотки дросселя без учёта эффекта уширения магнитного потока

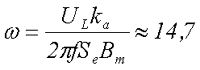
Полученный результат округлим до ближайшего целого, таким образом, количество витков примем ω = 15. С учетом этого определим величину немагнитного зазора сердечника δ

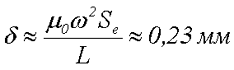
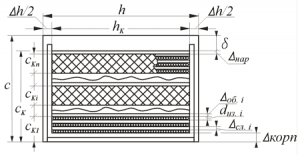
В связи с тем, что прокладка для создания немагнитного зазора прокладывается как между центральными кернами, так и между боковыми, то соответственно толщина прокладки необходимо уменьшить вдвое по сравнению с рассчитанным значением. То есть толщина прокладки должна составлять 0,1…0,12 мм.

В связи с наличием немагнитного зазора происходит уширение магнитного потока и как следствие увеличение индуктивности. Для того чтобы индуктивность дросселя L соответствовала заданной, необходимо пересчитать число витков обмотки ω с учётом коэффициента уширения F

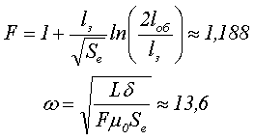
Таким образом, количество витков примем равным ω = 14. Для окончательного расчёта параметров дросселя определим сечение провода с учётом плотности тока j = 5 А/мм².

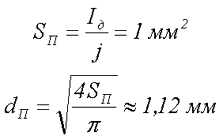
Как видно сечение провода составляет S_П = 1 мм², данному сечению соответствует провод диаметром d_П = 1,12 мм. Так как частота переменного тока дросселя достаточно высокая, то для снижения потерь мощности вследствие скин-эффекта необходимо использовать литцендрат – провод состоящий из нескольких жил. Диаметр жилы d_Ж не должен превышать удвоенной толщины скин-слоя ∆

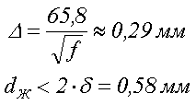
В связи с этим для обмотки можно использовать провод, скрученный из 9 жил диаметром 0,38 мм, имеющего суммарное сечение S_П = 1,02 мм².

4.Для завершения расчётов необходимо рассчитать температуру перегрева дросселя ∆Т. Для этого необходимо определить потери мощности в обмотке ∆Р₁ и в сердечнике ∆Р₂, также суммарную площадь охлаждения дросселя.

Мощность потерь в обмотке ∆P₁, зависит от удельного сопротивления проводника (q_Cu = 0,0171 (Ом•мм²)/м), длины обмоточного провода l_пр.об и температурного коэффициента сопротивления меди α_Cu = 0,0038 °C^-1.

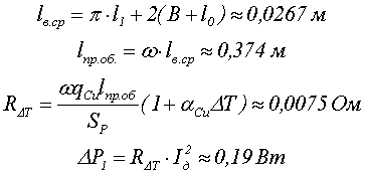
где l_в.ср. – средняя длина витка обмотки дросселя,

R_∆T – сопротивление провода при температуре перегрева.

Для определения потерь мощности в сердечнике ∆P₂ необходимо определить удельные объёмные потери P_V при заданной частоте f, рабочей температуре T и максимальной индукции, создаваемой переменным током в дросселе B_m.

По справочным данным для феррита марки N87, при B_m = 300 мТл, f = 50 кГц и T = 70 °C, объемные потери составляют P_V ≈ 250 кВт/м³ = 0,25•10^-3 Вт/мм³, тогда потери мощности в сердечнике объемом V_e = 2980 мм³ составят

Рассчитаем площади охлаждения сердечника S_С и площадь охлаждения обмотки S_O.

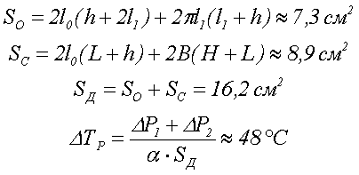
Таким образом, перегрев составляет ∆Т = 48 °С соответствует требуемым условиям, но находится на пределе, поэтому можно порекомендовать снизить максимальное значение индукции B_m путём увеличения количества витков обмотки, или использовать сердечник большего размера.