Всем доброго времени суток! Большинству электронных схем для правильной работы необходим постоянный ток. Однако выпрямительные устройства различных конструкций выдают напряжения, имеющие пульсирующую составляющую. Для уменьшения пульсаций между выпрямителем и нагрузкой ставят сглаживающий фильтр. В современных схемах роль такого фильтра выполняет электролитический конденсатор большой ёмкости, параллельный нагрузке. Во многих случаях его вполне достаточно, особенно при питании цифровых схем. Но при питании от емкостных фильтров аналоговых устройств или устройств с большим потребляемым током, импульсные помехи оказывают существенное влияние на работу устройства, а в особых случаях и выводит их из строя. Поэтому в дополнение к конденсатору ставят дроссель, последовательно с нагрузкой, что значительно улучшает режим работы устройства. Данная статья посвящена расчёту дросселей сглаживающих фильтров.
Для сборки радиоэлектронного устройства можно преобрески DIY KIT набор по ссылке.
Принцип работы дросселя фильтра
Сглаживающим дросселем или дросселем фильтра называется компонент электронной схемы, предназначенный для уменьшения переменной составляющей напряжения или тока на входе или выходе схемы. Он, как правило, состоит из замкнутого магнитопровода (сердечника) и одной обмотки. Обмотка дросселя включается последовательно с нагрузкой
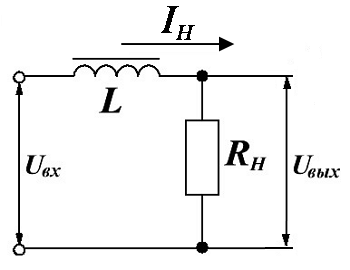
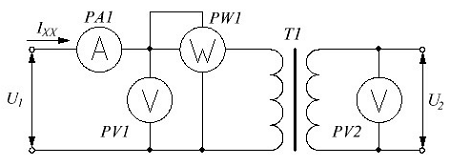
Схема включения дросселя фильтра.
Данный тип дросселя чаще всего входит в состав сложных многозвенных фильтров. Его действие основано на том, что активное сопротивление обмотки rдр намного меньше сопротивления нагрузки RН, а индуктивное сопротивление Хдр на частоте пульсаций f – намного больше, чем сопротивление нагрузки
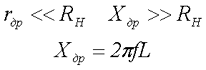
Таким образом, представляя напряжение на входе дросселя Uвх как сумму постоянной U0 и переменной составляющей U~, можно сделать вывод, что практически вся постоянная составляющая будет приложена к нагрузке, а переменная составляющая – к дросселю.
Качество любого фильтра оценивают с помощью коэффициента сглаживания, который для сглаживающего дросселя определяется по выражению
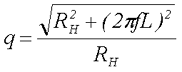
Из данного выражения, по необходимой величине коэффициента сглаживания q можно определить требуемое значение индуктивности дросселя L.
Физические процессы в сердечнике дросселя
Как уже говорилось, сглаживающий дроссель представляет собой катушку с ферромагнитным сердечником, который значительно увеличивает магнитное поля, поэтому все характеристики дросселя определяются свойствами сердечника. В тоже время свойства сердечника зависят от тока IL, протекающего через дроссель. Данный ток можно представить в виде суммы постоянной составляющую I0 и переменной составляющей I~.
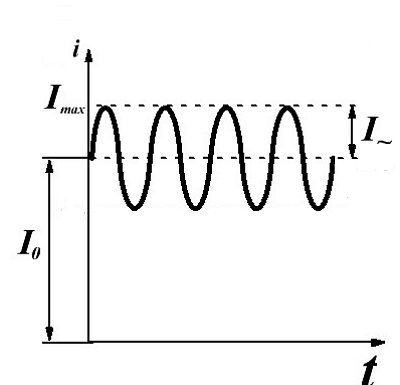
Ток, протекающий через дроссель фильтра.
В связи с этим можно выделить два параметра пульсирующего тока: амплитудное значение тока Imax и действующее значение тока I, которые определяются следующими выражениями
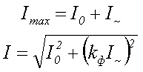
где I0 и I~ – соответственно амплитуда постоянной и переменной составляющей импульсного тока, протекающего через сглаживающий дроссель,
kф – коэффициент формы тока переменной составляющей.
Рассмотрим влияние пульсирующего тока на параметры сердечника. На рисунке ниже приведены кривые намагничивания сердечника для двух режимов: при отсутствии подмагничивания (I0 = 0) и с подмагничиванием постоянным током (I0 > 0).
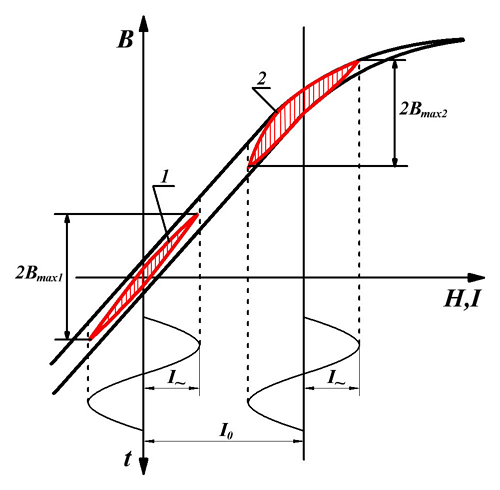
Работа дросселя при подмагничивании.
На рисунке изображены кривые изменения индукции магнитного поля в сердечнике при его намагничивании синусоидальным током при двух режимах работы: без подмагничивания (кривая 1) и с подмагничиванием постоянным током I0 (кривая 2). Как известно, при периодическом намагничивании сердечника магнитная индукция В изменяется не по основной кривой намагничивания, а по замкнутым кривым, называемым петлями перемагничивания (выделены красным цветом). В первом случае, когда отсутствует подмагничивание, петля симметрична относительно основной кривой намагничивания (петля 1). В случае наличия тока подмагничивания I0, перемагничивание сердечника идёт по так называемым частным петлям перемагничивания (петля 2). Частные петли перемагничивания характеризуются увеличенной площадью, что означает увеличение потерь в сердечнике (площадь ограниченная петлёй равна мощности потерь в сердечнике).
Кроме увеличения потерь при насыщении сердечника, происходит уменьшение магнитной проницаемости материала сердечника. Так как индуктивность дросселя L имеет прямую зависимость от магнитной проницаемости, то следовательно происходит снижение индуктивности.
Эквивалентная проницаемость вещества μе определяется из отношения между создаваемой магнитным полем индукцией В и напряженностью Н данного магнитного поля
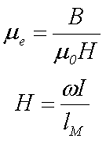
где ω – количество витков провода в обмотке,
I – ток через дроссель.
Индуктивность дросселя может быть определена по следующему выражению
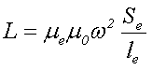
где ω – количество витков провода в обмотке,
μ0 – магнитная постоянная, μ0 = 4π*10-7 Гн/м,
μе – эквивалентная (относительная) магнитная проницаемость сердечника,
Sе – эквивалентная площадь поперечного сечения сердечника,
lе – эквивалентная длина магнитной линии сердечника.
lM – длина магнитной линии в сердечнике.
Дроссель фильтра с зазором в сердечнике
Для уменьшения падения магнитной проницаемости и индуктивности дросселя при увеличении подмагничивающего тока в сердечник дросселя вводят немагнитный зазор. Ниже представлены кривые намагничивания сердечника с зазором и без зазора.
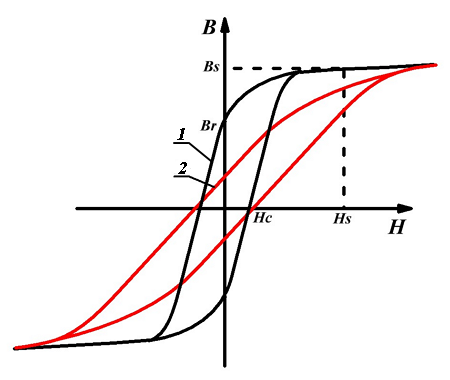
Кривые намагничивания материала сердечника: без зазора (1) и с зазором (2).
Как видно из рисунка петля гистерезиса сердечника без зазора – это линия 1, а петля гистерезиса сердечника, имеющего немагнитный зазор – это линия 2. То есть кривая 2 растягивается и поворачивается относительно нулевой координаты. Таким образом сердечник дросселя при наличии зазора, характеристика намагничивания которого линейна, насыщается при относительно больших токах в обмотке, чем сердечник без зазора.
Отсюда можно сделать вывод, что при увеличении тока подмагничивания необходимо выбирать большую величину немагнитного зазора для увеличения индуктивности дросселя.
Возникает вопрос выбора длины немагнитного зазора в сердечнике. В одной из статей я рассказывал, как рассчитать эквивалентную магнитную проницаемость при наличии зазора. Здесь стоит обратная задача – рассчитать длину зазора по некоторой заданной проницаемости, выражение будет иметь вид
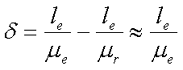
где δ – длина немагнитного зазора, мм,
le – эффективная длина магнитной силовой линии, мм,
μe – эффективная магнитная проницаемость сердечника с зазором,
μr – относительная магнитная проницаемость материала сердечника. Так как величина магнитной проницаемости материала сердечника, значительно больше, чем требуемая проницаемость μe << μr, то последнее слагаемое в выражении можно не учитывать.
Особенности расчёта дросселя фильтра
Расчёт дросселя фильтра в общем случае сводится к выбору конструкции, типоразмера и материала магнитопровода и параметров обмоток, для которых обеспечивается заданные параметры: индуктивности дросселя L, тока подмагничивания I0 и пульсаций переменной составляющей I~ заданной частоты f. При этом перегрев дросселя ∆T не должен превышать заданное значение.
Индуктивность дросселя L и протекающий ток Imax определяет максимальное значение энергии магнитного поля дросселя. При этом энергия дросселя определяется следующим выражением
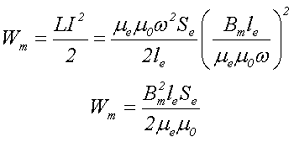
где ω – количество витков провода в обмотке,
μ0 – магнитная постоянная, μ0 = 4π*10-7,
μе – эффективная магнитная проницаемость сердечника,
Se – эффективная площадь поперечного сечения сердечника,
le – эффективная длина магнитной линии сердечника,
Bm – максимальное значение индукции магнитного поля в сердечнике.
Здесь необходимо дать некоторые пояснения:
— во-первых, все размерности необходимо приводить к общему виду, например, Se и le в справочниках приводятся в миллиметрах и квадратных миллиметрах, соответственно, их необходимо переводить в метры и квадратные метры;
— во-вторых, максимальное значение индукции Bm магнитного поля зависит от типа применяемого материала сердечника. В свою очередь тип применяемого материала зависит от частоты, например, при частотах 50 Гц – 10 кГц, применяют электротехнические стали, на частотах 5 – 30 кГц – электротехнические сплавы (например, аморфные), от 10 кГц и выше – ферриты и магнитодиэлектрики. Однако данное разделение в некоторой степени условно, так как применение конкретного материала ограниченно потерями в нем на гистерезис (перемагничивание) и вихревые токи;
— в-третьих, максимальное значение индукции в сердечнике Bm следует выбирать исходя из следующего ограничения
![]()
где BS – индукция насыщения материала магнитопровода.
Данное ограничение связано с возможными бросками тока в цепи и другими негативными факторами, например изменение температуры и влажности сердечника.
Для определения параметров обмотки введём понятие коэффициента использования окна сердечника kИ, который определяет количество меди, появляющееся в площади окна дросселя. На данный коэффициент влияют следующие факторы:
— толщина изоляции обмоточного провода, так в зависимости от диаметра провода площадь изоляции занимает от 5 до 30 % от площади сечения провода;
— способ укладки провода в окне (рядовая обмотка или внавал);
— толщина межслоевой изоляции в многослойных и многообмоточных конструкциях;
— качеством намотки обмотки.
С учётом данных факторов коэффициент использования окна сердечника kИ превышает 30 % или 0,3, что необходимо учитывать при выборе сердечника. Поэтому ещё одним ограничением для размеров сердечника является площадь окна SO и зависимость от данного параметра плотности тока j, площади сечения провода SP и количества витков провода ω, которые объединены следующим выражением
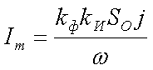
где kи – коэффициент использования окна сердечника,
SO – площадь окна сердечника,
ω – количество витков провода в обмотке.
С помощью данного выражения можно определить требуемую эквивалентную магнитную проницаемость сердечника
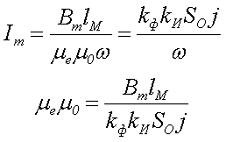
Подставив полученное выражение в формулу для максимальной энергии получим
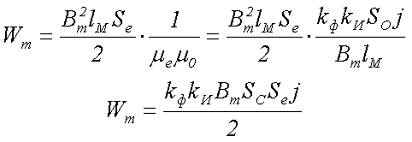
Отсюда можно выразить произведение SeSO, которое определяет геометрию сердечника дросселя
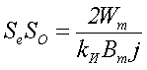
После выбора сердечника необходимо определить эквивалентную магнитную проницаемость сердечника согласно выражению
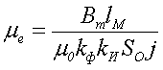
Далее определяют длину немагнитного зазора и параметры обмотки: количество витков ω, диаметр провода dp, средняя длина витка lср.вит. и сопротивление обмотки R.
По окончанию расчёта необходимо провести проверку не величину перегрева дросселя ∆T и в случае необходимости скорректировать размер сердечника: при слишком большом перегреве необходимо выбрать больший размер сердечника.
Потери мощности в дросселе фильтра
Несколько слов необходимо сказать об особенностях учёта потерь мощности в дросселе фильтра, так как они определяют температуру нагрева и перегрева дросселя. Для упрощения расчётов можно выделить два случая:
— в первом случае, переменная составляющая тока I~ меньше постоянного тока подмагничивания I0 дросселя (I~<< I0). В этом случае потери мощности определяются только потерями в обмотке дросселя
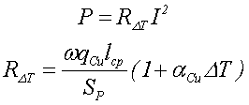
где R∆T – сопротивление обмотки при температуре перегрева,
I – действующее значение тока дросселя,
ω – число витков обмотки дросселя,
lср – средняя длина витка в обмотке,
SP – площадь сечения провода «по меди»,
qCu – удельное сопротивление потерь для меди, qCu = 0,0171 Ом*мм2/м,
αCu – температурный коэффициент сопротивления меди, αCu = 0,0038 °С-1.
— во втором случае, когда переменная составляющая тока дросселя I~ значительна, нельзя не учитывать потери мощности в сердечнике. Данные потери связанны с перемагничиванием сердечника и токами Фуко, поэтому учитывается только амплитуда переменной составляющей магнитной индукции B~
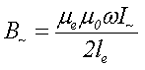
Далее по полученному значению амплитуды магнитной индукции необходимо определить удельные объемные потери на перемагничивание PV и в зависимости от объёма сердечника Ve определить потери мощности в сердечнике.
Расчёт дросселя фильтра
В качестве примера рассчитаем дроссель, имеющий индуктивность L = 70 мкГн, ток подмагничивания I0 = 12 А, амплитуда переменной составляющей I~ = 1 А, частота пульсаций f = 100 кГц, температура перегрева ∆Т = 50°С, форма тока имеет вид представленный ниже, поэтому коэффициент формы тока kф ≈ 1,732
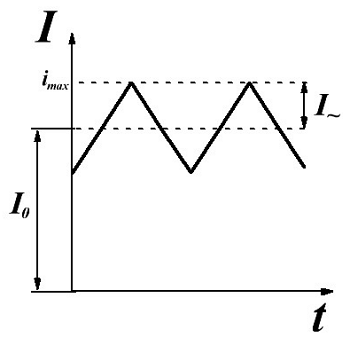
Ток в обмотке дросселя.
1. Вначале определяем размер сердечника, который может накапливать необходимую энергию Wm. В качестве материла магнитопровода используем материал N87, поэтому максимальную индукцию примем равной Bm = 0,3 Тл, коэффициент использования окна сердечника kИ = 0,3 и плотность тока j = 5 А/мм2
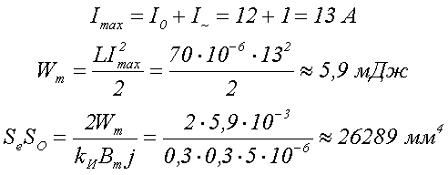
По итогам расчётов, выберем сердечник EE40/16/12 фирмы Epcos, имеющего следующие параметры le = 154 мм, Se = 149 мм2, SO = 169 мм2, Ve = 22946 мм3 материал сердечника N87 (μe = 1710).
2. Теперь необходимо рассчитать параметры обмотки: сечение провода «по меди» SP и количество витков обмотки ω. Сечение провода выбирается исходя из допустимой плотности тока j
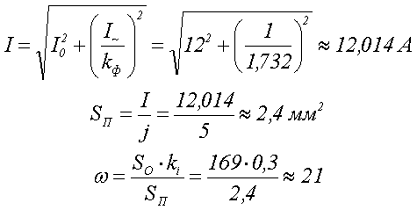
Сечение провода получилось равным SП = 2,4 мм2, так как частота переменной составляющей f = 100 кГц, то для снижения потерь мощности на скин-эффект применим литцендрат типа ЛЭШО 615х0,071, имеющий общее сечение SП = 2,43 мм2. Литцендрат можно изготовить самостоятельно, для этого провод составляют из нескольких жил провода типа ПЭВ-2 или ПЭТВ-2. При этом максимальный диаметр жилы dП зависит от глубины скин-слоя δ
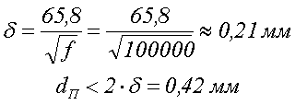
В качестве жил выберем провод ПЭВ-2 0,3, при этом площадь сечения одной жилы Sж и количество жил N составит
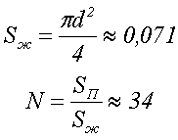
3. Рассчитаем требуемую эквивалентную магнитную проницаемость μe и толщину немагнитного зазора в сердечнике δ
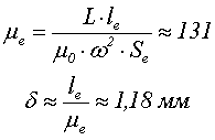
Следовательно, эквивалентная проницаемость сердечника составит μe = 131, а длина немагнитного зазора δ=1,18 мм. Прокладка между кернами сердечника должна быть вдвое меньше длины зазора, так как она прокладывается, как между центральными, так и между боковыми кернами.
Теперь необходимо проверить правильность расчётов по параметру допустимого перегрева. Для этого необходимо рассчитать мощность потерь в обмотке и в сердечнике, а также площади поверхностей обмотки и сердечника.
4. Рассчитаем мощность потерь в обмотке ∆P1. Для этого необходимо определить среднюю длину витка lв.ср, длину провода обмотки lпр.об и сопротивление провода при перегреве ∆T = 50 °С. В данных расчётах необходимо учитывать удельное сопротивление меди qCu = 0,0171 (Ом•мм2)/м и температурный коэффициент сопротивления меди αCu = 0,0038 °C-1
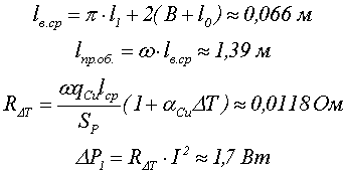
5. Рассчитаем мощность потерь в сердечнике ∆P2. Для этого необходимо определить удельные объёмные потери в сердечнике на данной частоте, температуре и индукции
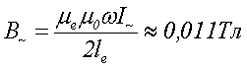
Для нахождения удельных объёмных потерь PV обратимся к справочным данным на феррит марки N87, для которого при B~ = 11 мТл, f = 100 кГц и T = 100 °C, объемные потери составляют PV ≈ 0,4 кВт/м3 = 4•10-7 Вт/мм3, тогда потери мощности в сердечнике, объемом Ve = 22946 мм3 составят
![]()
6. Осталось рассчитать площадь охлаждения дросселя SД и определить расчётный перегрев дросселя ∆TP. Для этого воспользуемся значением коэффициента теплопередачи α = 1,2*10-3 Вт/(°С см2) и переведём значение площадей охлаждения в квадратные сантиметры
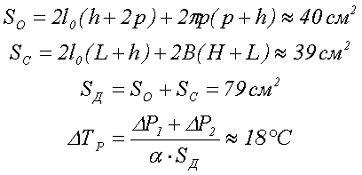
Таким образом, перегрев дросселя составляет ∆T = 18 °C, что соответствует требованиям начальных условий. Так как величина перегрева почти в 3 раза меньше требуемой, то размер сердечника можно уменьшить, а его параметры пересчитать задавшись большей плотностью тока, например, 6-7 А/мм2. И заново рассчитать параметры дросселя и проверить по величине перегрева.
Теория это хорошо, но необходимо отрабатывать это всё практически ПОПРОБОВАТЬ МОЖНО ЗДЕСЬ

 Режимы работы трансформатора. Часть 1
Режимы работы трансформатора. Часть 1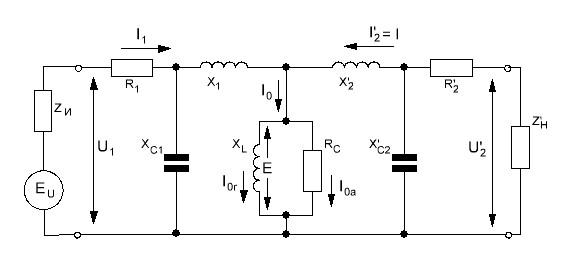 Эквивалентная схема трансформатора
Эквивалентная схема трансформатора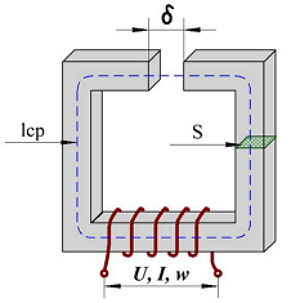 Катушки индуктивности с малым воздушным зазором
Катушки индуктивности с малым воздушным зазором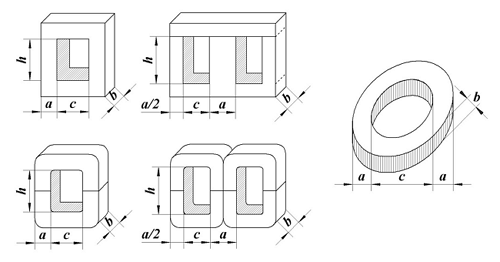 Выбор и параметры сердечника трансформатора
Выбор и параметры сердечника трансформатора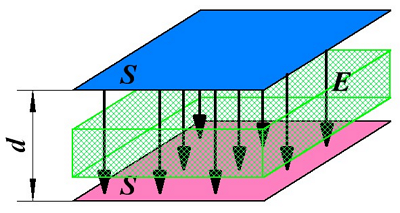 Принцип работы и устройство конденсатора
Принцип работы и устройство конденсатора