Всем доброго времени суток! Продолжаем работу с NI Multisim. Сегодня будем рассматривать и исследовать разветвлённые цепи постоянного тока. Исследуем мост постоянного тока, широко используемый в измерительном оборудовании. Рассмотрим цепь с несколькими источниками напряжения. Найдём токи и напряжения в ветвях и на участках разветвлённой цепи.
Мост постоянного тока
Использование моста сопротивлений для измерения электрических и неэлектрических величин связано с тем, что он уменьшает или полностью убирает погрешности от сопротивлений соединительных проводников. Также он обеспечивает напряжение, которое пропорционально измеряемому сопротивлению. Схема измерительного моста представлена ниже
Для сборки радиоэлектронного устройства можно преобрески DIY KIT набор по ссылке.
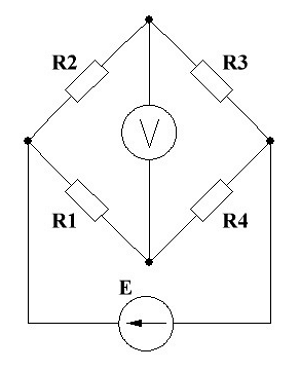
Измерительный мост постоянного тока.
Для равновесия моста необходимо, что произведение его противоположных плеч было одинаково
Данное выражение называют условием равновесия моста.
Тогда для определения величины сопротивления любого резистора, например, R2, используется выражение
При уравновешенном мосте при небольшом изменении сопротивления резистора в любом из плечей, например ΔR4, напряжение на вольтметре, включённом в диагональ моста, составит
Измерительные мосты характеризуются чувствительностью:
— абсолютная чувствительность (в мВ/Ом), определяется как отношение приращений напряжения ΔU к приращению измеряемого сопротивления ΔR
— относительная чувствительность (в мВ), определяется как отношение приращения напряжения ΔU к относительному изменению сопротивления моста ΔR/R4
где ΔU = Un+1 – Un – приращение выходного напряжения в диагонали моста, вызванное изменением сопротивления плеча моста ΔR.
Соберём схему измерительного моста постоянного тока в NI Multisim со следующими параметрами схемы:
— сопротивления резисторов R1 = R3 = 1 кОм;
— сопротивления потенциометров R2 = R4 = 1 кОм;
— источник напряжения идеальный (Rвн = 0) с ЭДС Е = 12 В;
— вольтметр: род тока (mode) – постоянный (DC), внутреннее сопротивление (Resistance) RV = 1 Мом.
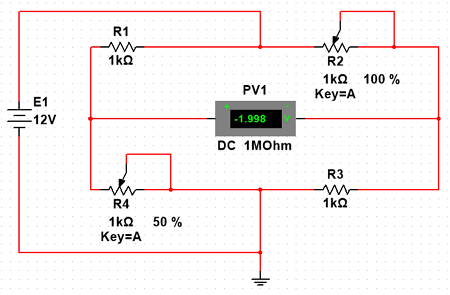
Схема в Multisim, моделирующая работу измерительного моста постоянного тока.
Рассмотрим, как будут изменяться параметры измерительного моста при изменении сопротивления R4, для этого будем запускать моделирование при следующих параметрах: R1 = R2 = R3; R4 = (R1 — nΔR), где n = 0,…,5, ΔR = 0,05 Ом. Результаты измерений занесём в таблицу ниже
| n | R1=R2=R3 | R4 = (R1 — nΔR) | U, мВ | Sa, мВ/Ом | So, мВ |
| 0 | 1 кОм | 1 кОм | 0 | — | — |
| 1 | 1 кОм | 950 Ом | 154 | 3,08 | 2926 |
| 2 | 1 кОм | 900 Ом | 315 | 3,22 | 2898 |
| 3 | 1 кОм | 850 Ом | 486 | 3,42 | 2907 |
| 4 | 1 кОм | 800 Ом | 666 | 3,6 | 2880 |
| 5 | 1 кОм | 750 Ом | 856 | 3,8 | 2850 |
На основе этих данных построим графики абсолютной и относительной чувствительности моста по напряжению в зависимости от изменения сопротивления R4.

Зависимость абсолютной чувствительности моста от сопротивления.

Зависимость относительной чувствительности моста от сопротивления.
Повторим данный опыт ещё раз, только изменяя величину двух сопротивлений R2 и R4.
| n | R1=R3 | R2=R4 = (R1 — nΔR) | U, мВ | Sa, мВ/Ом | So, мВ |
| 0 | 1 кОм | 1 кОм | 0 | — | — |
| 1 | 1 кОм | 950 Ом | 307 | 6,14 | 5833 |
| 2 | 1 кОм | 900 Ом | 631 | 6,48 | 5832 |
| 3 | 1 кОм | 850 Ом | 972 | 6,82 | 5797 |
| 4 | 1 кОм | 800 Ом | 1332 | 7,2 | 5760 |
| 5 | 1 кОм | 750 Ом | 1713 | 7,62 | 5715 |
Графические зависимости между чувствительностью и сопротивлениями представлены ниже.

Зависимость абсолютной чувствительности моста от сопротивления.

Зависимость относительной чувствительности моста от сопротивления.
Линейная цепь с двумя источниками напряжения
В качестве такой цепи рассмотрим двухконтурную цепь с двумя источниками положительного напряжения. В её состав входят: два источника ЭДС Е1 и Е2 со своими внутренними сопротивлениями RВН1 и RВН2, а также общая нагрузка цепи R.
При анализе данной цепи выполняют следующие расчёты:
- Рассчитывают токи в ветвях, используя различные методы (законы Кирхгофа, метод наложения, метод контурных токов, метод двух узлов). Для расчёта будем использовать законы Кирхгофа. В соответствии с первым законом сумма токов в любом узле цепи равна нулю
По второму закону Кирхгофа сумма напряжений на резистивных элементах в контуре равна сумме ЭДС в данном контуре
Из этих трёх выражений составим систему уравнений и решим.
- Рассчитывают мощность, потребляемую нагрузкой, а также баланс мощностей. Мощность, которую потребляет нагрузка составляет
Условие баланса мощностей состоит в том, что алгебраическая сумма мощностей, развиваемая источниками энергии, равна сумме мощностей, потребляемой нагрузкой и затрачиваемой внутри источников энергии. То есть для нашей схемы должно выполняться равенство
Знак «±» показывает, что «+» ставится, когда направление ЭДС EK и IK источника совпадают, а «-» — при их противоположном направлении.
- Построение потенциальной диаграммы контура. Потенциальной диаграммой контура, называется распределение потенциалов узлов схемы в зависимости от сопротивлений элементов контура, то есть φ = f(R).
Для построения потенциальной диаграммы необходимо знать величину и направление токов в ветвях контура и ЭДС источников напряжения. Далее в соответствии с изображением ниже выделим четыре узла: a, b, c, d. Заземлим узел a (то есть примем узел а = 0 В) и обойдём внешний контур.
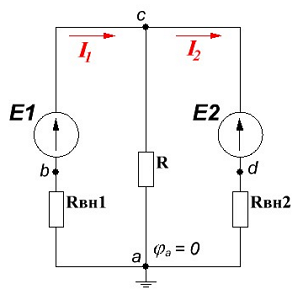
Схема цепи для построения потенциальной диаграммы контура.
Тогда потенциал узла а
Потенциал узла b
Потенциал узла с
Потенциал узла d
Потенциал узла a
При возвращении в исходную узловую точку a с нулевым потенциалом после расчёта потенциалов всех точек вдоль выбранного контура подтверждает правильность расчёта цепи.
Пример расчёта цепи с двумя источника питания
В качестве примера рассмотрим двухконтурную цепь с двумя источниками питания со следующими параметрами: E1 = 15 В, RВН1 = 1,5 Ом, R = 20 Ом, E2 = 13 В, RВН2 = 7 Ом.
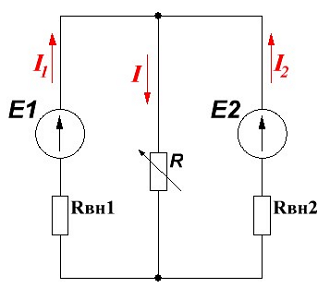
Двухконтурная цепь с двумя источниками питания.
-
- Составим систему уравнений токов и напряжений и найдём величину токов в цепях
-
- Рассчитаем мощность, потребляемую нагрузкой R и составим баланс мощностей
Таким образом, баланс мощностей соблюдается.
- Построим потенциальную диаграмму наружного контура для этого заземлим узел а, то есть
Потенциал узла b
Потенциал узла с
Потенциал узла d
Потенциал узла a
Построим потенциальную диаграмму в соответствие с получившимися данными
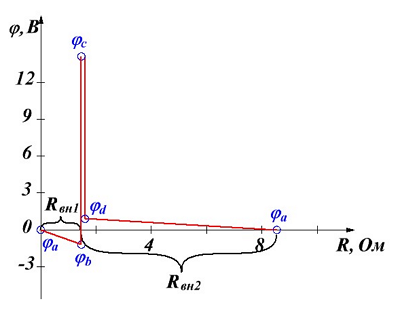
Потенциальная диаграмма двухконтурной цепи с двумя источниками питания.
Исследование двухконтурной цепи в среде Multisim
Соберём на рабочем поле среды Multisim схему для испытания двухконтурной схемы цепи постоянного тока.
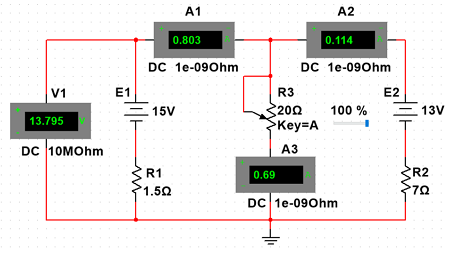
Схема для испытания двухконтурной цепи постоянного тока в среде Multisim.
Для исследования данной схемы данные полученные в ходе экспериментов будем записывать в таблицу ниже.
| Измерено при сопротивлении нагрузки R, Ом | R, Ом | I1, А | I2, А | I3, А | U1, В | P, Вт |
| ∞ | 0,24 | 0,24 | 0 | 14,65 | 0 | |
| 10R | 0,3 | 0,22 | 0,07 | 14,56 | 1,07 | |
| 5R | 0,35 | 0,21 | 0,15 | 14,47 | 2,1 | |
| 2R | 0,53 | 0,17 | 0,36 | 14,21 | 5,04 | |
| R | 0,8 | 0,11 | 0,69 | 13,8 | 9,52 | |
| 0,75R | 0,98 | 0,076 | 0,9 | 13,53 | 12,2 | |
| 0,5R | 1,31 | 0,005 | 1,3 | 13,04 | 17 | |
| 0,25R | 2,17 | -0,18 | 2,35 | 11,75 | 27,59 | |
| 0 | 10 | -1,86 | 11,86 | 0 | 0 | |
| Расcчитано при R | 0,8 | 0,11 | 0,69 | 13,8 | 9,52 | |
Построим внешнюю характеристику источника Е1: зависимости напряжения U1 от протекающего тока I1, то есть
Для этого изменяем величину сопротивления R3 (на схеме Multisim) от режима холостого хода (R3 = ∞) до режима короткого замыкания (R3 = 0), а данные записываем в таблицу.
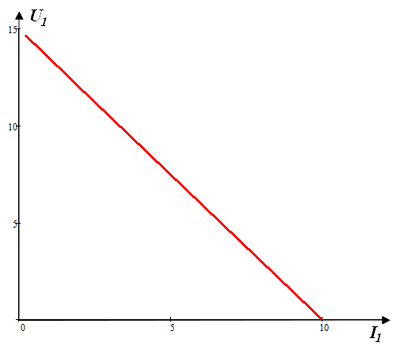
График внешней характеристики источника напряжения Е1.
Двух контурная цепь с двумя источниками напряжения является одним из частных случаев широко распространённой практической схемы линейной разветвлённой цепи. Рассмотрим, как провести анализ и исследуем такую цепь.
Анализ линейной разветвлённой цепи постоянного тока
В основе анализа линейной разветвлённой электрической цепи постоянного тока лежит расчёт токов в ветвях и напряжений на различных участках цепи. Для расчёта различного вида электрических цепей применяют метод узловых потенциалов (напряжений) МУП или метод контурных токов МКТ.
При расчёте этими методами составляются и решаются системы уравнений, где количество уравнений в системе определяются следующими выражениями
где В – количество ветвей (без учёта ветвей с источниками тока) в схеме,
У – количество узлов в электрической схеме.
В качестве примера покажем расчёт следующей схемы методом узловых потенциалов.
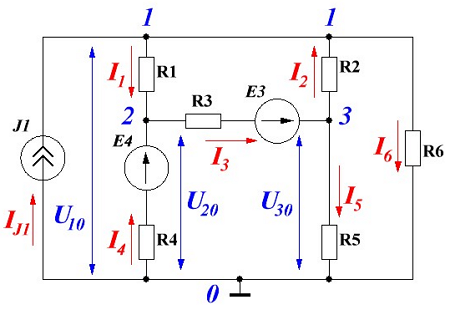
Пример схемы линейной разветвлённой электрической цепи.
Для анализа цепи примем следующие исходные данные: E3 = 35 В, Е4 = 10 В, J1 = 5 А, R1 = 4 Ом, R2 = 2 Ом, R3 = 7 Ом, R4 = 4 Ом, R5 = 2 Ом, R6 = 1 Ом.
Рассмотрев топологию данной схемы можно рассмотреть в ней 7 ветвей, 4 узла, 3 независимых контура, и 6 неизвестных токов. Таким образом для расчёта данных токов необходимо составить систему из
где У – количество узлов в схеме.
Таким образом необходимо составить систему из 3 уравнений. Для этого выбираем базисный узел (узел 0) и составим систему уравнений:
где G11, G22, G33 – сумма проводимостей всех ветвей, входящих в соответствующий узел;
G12, G13, G21, G23 G31, G32 – сумма проводимостей ветвей, соединяющих соответствующие узлы;
G3, G4 – проводимости соответствующих сопротивлений;
I11, I22, I33 – токи соответствующих узлов.
Ток узла Ikk – равен алгебраической сумме токов, полученных от деления ЭДС ветвей, подходящих к узлу, на сопротивление этих ветвей. Если ЭДС направлена от узла, то она берётся со знаком «-», а если к узлу, то со знаком «+». Аналогично поступают, если к узлу подходит источник тока. Тогда токи узлов составят
Вычислим соответствующие проводимости:
Таким образом система уравнений имеет вид
Решив данную систему уравнений получим значение потенциалов в узловых точках:
Вычислить токи в ветвях можно по обобщённому закону Ома с учётом выбранных направлений токов в ветвях.
Произведём проверку правильности расчёта токов, используя первый закон Кирхгофа для одного из узлов, например, узла 1.
Исследование линейной разветвлённой цепи постоянного тока в среде Multisim
Соберём на рабочем поле среды Multisim схему для испытания линейной разветвлённой цепи постоянного тока.
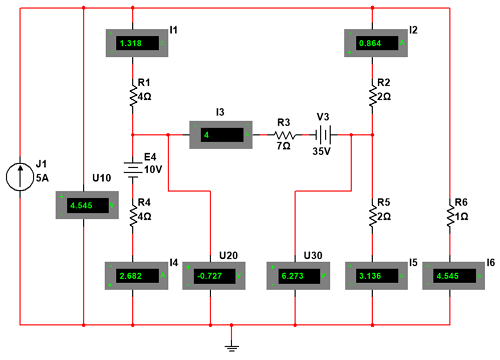
Схема для исследования линейной разветвлённой цепи постоянного тока.
| Узловые напряжения | Токи ветвей схемы | ||||||||
| U10, B | U20, B | U30, B | I1, A | I2, A | I3, A | I4, A | I5, A | I6, A | |
| Рассчитано | 4,545 | -0,727 | 6,273 | 1,318 | 0,864 | 4 | 2,682 | 3,136 | 4,545 |
| Измерено | 4,545 | -0,727 | 6,273 | 1,318 | 0,864 | 4 | 2,682 | 3,136 | 4,545 |
Теория это хорошо, но необходимо отрабатывать это всё практически ПОПРОБОВАТЬ МОЖНО ЗДЕСЬ

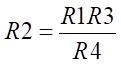
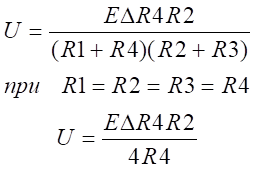
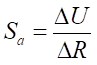
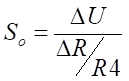
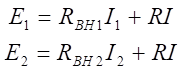
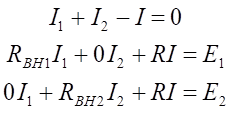
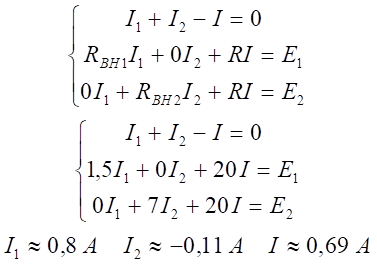
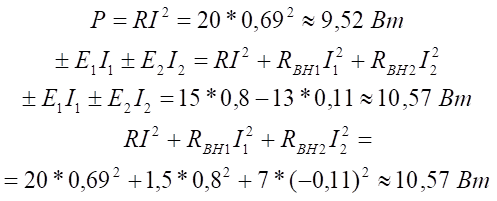
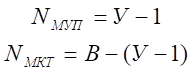
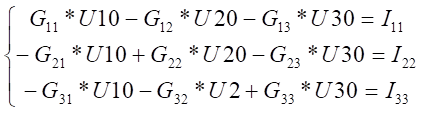
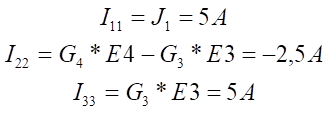
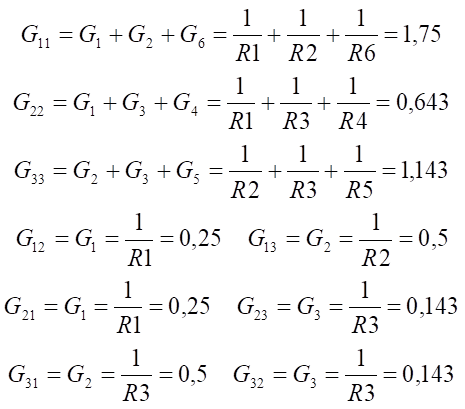
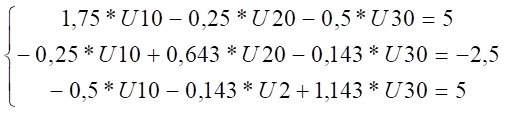
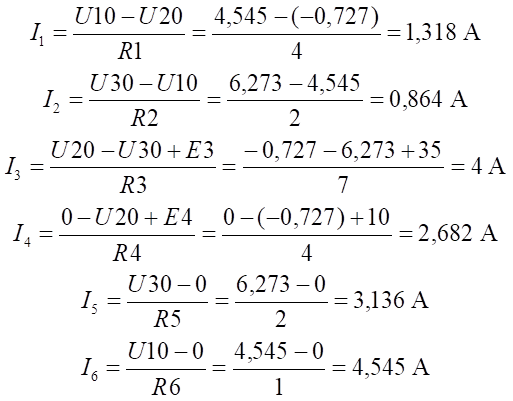
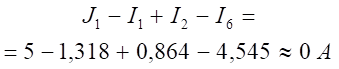
 NI Multisim. Измерение электрических величин
NI Multisim. Измерение электрических величин Установка и интеграция curl
Установка и интеграция curl