ElectronicsBlog

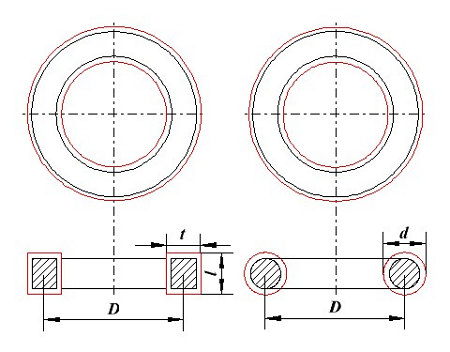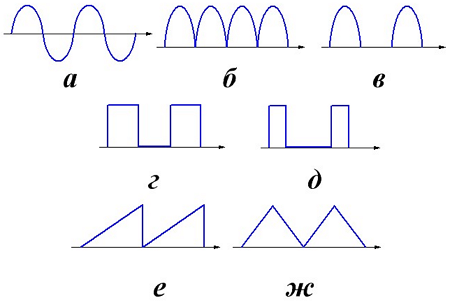
Всем доброго времени суток! В прошлой статье я рассказывал о дросселе и его параметрах. В частности рассмотрел межвитковую ёмкость и индуктивность рассеивания обмоток. Данные параметры влияют на реактивную мощность дросселя, кроме потерь реактивной мощности в дросселе присутствуют параметры, вызывающие потери активной мощности. Это во-первых, сопротивление обмоточного провода дросселя и активные потери в сердечнике. Данная статья посвящена активным потерям в обмотках дросселя.

На характеристики дросселя кроме собственной индуктивности дросселя L, являющейся основным параметром, так сказать полезным, присутствует паразитная индуктивность Ls, обусловленная потоком рассеяния, активное сопротивление R обмоточного провода, межвитковая ёмкость С обмотки дросселя, а также проводимости g. Проводимость gμ характеризует мощность, которая затрачивается на перемагничивание сердечника, из-за наличие петли гистерезиса.

Реальные электронные компоненты (резисторы, катушки индуктивности, конденсаторы) кроме своих основных параметров (сопротивления, индуктивности и ёмкости) имеют так называемые паразитные параметры, например, конденсаторы имеют паразитные параметры обусловленные сопротивлением выводов и обмоток, а также их индуктивность, которые соединены последовательно – параллельно. Такие паразитные параметры образуют различные цепи, которые при воздействии переменного напряжения вызывают различные изменения переменного тока, а следовательно и мощности.

Цепи переменного напряжения характеризуются следующими параметрами: сопротивление R, индуктивность L и ёмкость С. Они оказывают влияние на параметры, характеризующие данную цепь: мощность, фазы тока и напряжения и др. Так в сопротивлении электрическая энергия переходит в теплоту, согласно закону Джоуля-Ленца, в индуктивности – энергия накапливается в магнитном поле, а в ёмкости – энергия накапливается в электрическом поле.

Как известно электрическим током называется упорядоченное движение заряженных частиц, которое возникает под действием разности потенциалов или напряжения. Одной из основных характеристик любого типа напряжения является его зависимость от времени. В зависимости от данной характеристики различают постоянной напряжение, значение которого с течением времени практически не изменяется и переменное напряжение, изменяющееся во времени. Переменное напряжение в свою очередь бывает периодическим и непериодическим. Периодическим называется такое напряжение, значения которого повторяются через равные промежутки времени. Непериодическое напряжение может изменять своё значение в любой период времени

Если магнитное поле возникает в сердечнике, имеющем воздушный зазор lз сопоставимый с длиной магнитной силовой линии в сердечнике lc. То в нём возникает размагничивающее поле, противоположное основному. Данное поле характеризуется размагничивающим фактором N или коэффициентом размагничивания. Данный фактор зависит от формы и размеров самого сердечника. Для учёта размагничивающего фактора на магнитные свойства сердечника ввели понятие эффективной магнитной проницаемости сердечника μе, которая зависит от магнитной проницаемости вещества сердечника μr и размагничивающим фактором N.

В прошедших статьях я рассказывал о расчёте индуктивности катушек без сердечников и катушек с замкнутыми сердечниками. Сегодняшняя статья посвящена катушкам индуктивности на разомкнутых сердечниках. Такие сердечники можно разделить на два типа: сердечники с малым зазором (δ << a), где δ – величина зазора намного меньше а – любого линейного размера сердечника и сердечники с большим зазором (δ ≥ а), где величина воздушного зазора δ больше или сопоставима с линейными размерами сердечника а. В данной статье разберём сердечники с малыми зазорами.

Всем доброго времени суток. В первой части я рассказал, как рассчитать индуктивность катушек с замкнутыми сердечниками тороидального и П-образного типа. Данная статья продолжает тему индуктивности катушек с замкнутыми сердечниками, здесь я расскажу о расчёте катушек с Ш-образными и броневыми сердечниками.

В отличие от индуктивных элементов без сердечников, при расчёте которых учитывался магнитный поток пронизывающий только проводник с током, магнитный поток индуктивных элементов с сердечниками практически полностью замыкается на сердечники. Поэтому при расчёте индуктивности таких элементов необходимо учитывать размеры сердечника и материал, из которого он изготовлен, то есть его магнитную проницаемость. Для сердечников, имеющих сложную конструктивную конфигурацию, вводится понятие эффективных (эквивалентных) размеров, которые учитывают особенности формы сердечников: эффективный путь магнитной линии le и эффективная площадь поперечного сечения Se сердечника.

В прошлых статьях я рассмотрел индуктивные элементы без сердечников, в частности, индуктивность прямого провода, индуктивность кольца и индуктивности различных типов круговых катушек. После этого можно было бы переходить к рассмотрению индуктивных элементов с сердечниками различной формы, однако существует ещё несколько типов катушек особой формы. Это, прежде всего, прямоугольные катушки и тороидальные катушки.