Всем доброго времени суток! В прошлой статье я рассказал о катушках индуктивности на сердечниках с малым магнитным зазором (длина зазора δ меньше любого линейного размера сердечника). Кроме сердечников с малым зазором существует сердечники, имеющие воздушный зазор сопоставимый с линейными размерами самого сердечника. Такие сердечники называются разомкнутыми. Данная статья описывает расчёт и параметры стержневых сердечников, являющихся разомкнутыми.
Для сборки радиоэлектронного устройства можно преобрески DIY KIT набор по ссылке.
Факторы, влияющие на индуктивность катушки на разомкнутом сердечнике
В сердечниках с малым воздушным зазором магнитное поле практически всё сосредоточенно в сердечнике, и в воздушном зазоре рассеивание магнитного поля незначительно. Другая картина возникает, если магнитное поле возникает в сердечнике, имеющем воздушный зазор lз сопоставимый с длиной магнитной силовой линии в сердечнике lc.
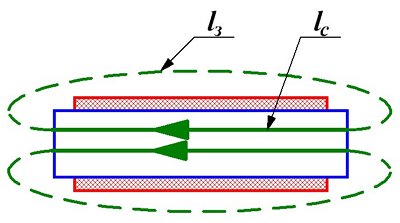
Магнитное поле в разомкнутом сердечнике.
Таким образом, магнитные сопротивления сердечника и воздушного зазора становятся соизмеримыми, что приводит к усложнению расчётных выражений для индуктивности катушек на таких сердечниках. В этом случае расчёт параметров ведут с учётом того, что в разомкнутых сердечниках на торцах сосредотачиваются противоположно ориентированные магнитные частицы, то есть частицы с положительным доменом смещаются в направлении внешнего поля, а отрицательные навстречу ему. В результате возникает размагничивающее поле, противоположное основному. Данное поле характеризуется размагничивающим фактором N или коэффициентом размагничивания. Данный фактор зависит от формы и размеров самого сердечника. Влияние размагничивающего фактора на магнитное поле сердечника описывается следующим выражением
![]()
где Н – напряженность магнитного поля в сердечнике,
Н0 – напряженность внешнего магнитного поля, то есть поля создаваемого катушкой, намотанной на разомкнутый сердечник,
НР – размагничивающее поле сердечника,
N – размагничивающий фактор,
J – вектор намагничивания сердечника.
Точное значение размагничивающего фактора, возможно, рассчитать только для однородно намагниченных тел, например, эллипсоидов вращения, шаров, дисков. Для учёта размагничивающего фактора на магнитные свойства сердечника ввели понятие эффективной магнитной проницаемости сердечника μе, которая зависит от магнитной проницаемости вещества сердечника μr и размагничивающим фактором N. Значение эффективной магнитной проницаемости сердечника для однородно намагниченных тел определяется следующим выражением
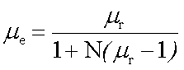
Однако в практике, используются неоднородно намагниченные тела – цилиндры, призмы, поэтому для расчёта эффективной магнитной проницаемости таких сердечников применяются эмпирически выведенные выражения.
Вследствие того, что значение размагничивающего фактора в неоднородно намагничиваемых телах различно по длине, то необходимо учитывать и расположение катушки индуктивности относительно сердечника и длину данной катушки относительно длины сердечника.
Таким образом, индуктивность катушки, выполненной на разомкнутом сердечнике можно определить по следующему выражению
![]()
где L0 – индуктивность катушки без сердечника, расчет смотреть (Часть 1, Часть 2, Часть 3),
μе – эквивалентная магнитная проницаемость разомкнутого сердечника,
k– коэффициент зависящий от отношения длины катушки к длине сердечника,
pl – коэффициент зависящий от расположения катушки относительно середины длины сердечника.
Рассмотри более подробно зависимость индуктивности от различных факторов.
Расчёт размагничивающего фактора
Как я уже говорил, размагничивающий фактор N зависит от размеров сердечника
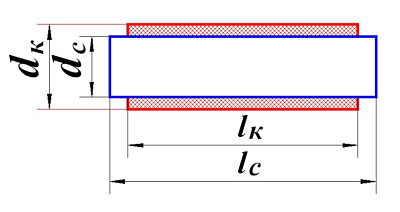
Катушка индуктивности с разомкнутым сердечником
Для его определения введём коэффициент λ, зависящий от отношения длины сердечника lc к его диаметру dc
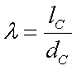
Тогда в интервале 2 ≤ λ ≤ 50 с точностью 10 % размагничивающий фактор данного сердечника можно определить по следующему выражению
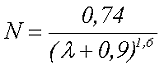
где λ – отношение длины сердечника к диаметру сердечника
Тогда эффективная магнитная проницаемость разомкнутого сердечника можно рассчитать по следующей формуле
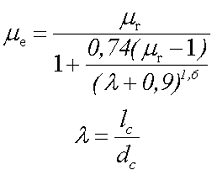
где μr – относительная магнитная проницаемость вещества сердечника,
lc – длина сердечника,
dc – диаметр сердечника.
Как влияет форма сердечника на магнитную проницаемость?
Эмпирическая формула вычисления эквивалентной магнитной проницаемости сердечников предполагает, что сечение сердечника представляет собой круг, но существует большое количество сердечников с не круглым сечением (прямоугольные, трубчатые).
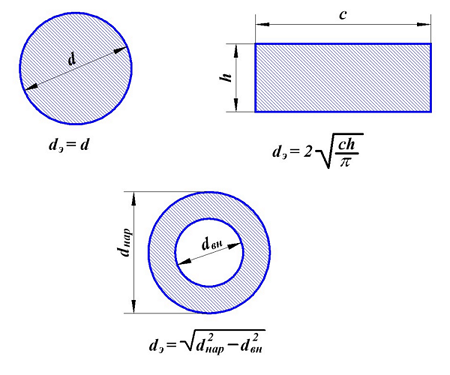
Вычисление эквивалентных диаметров сердечника.
Для упрощения расчётов все сердечники необходимо приводить к эквивалентному круговому сечению согласно следующим выражениям:
для прямоугольного сечения
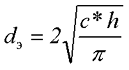
где с – ширина сердечника,
h – высота сердечника.
для трубчатого сечения
![]()
где dнар – наружный диаметр сердечника,
dвн – внутренний диаметр сердечника.
Влияние расположение катушки индуктивности относительно сердечника
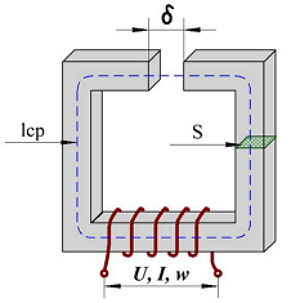
Довольно часто стержневые сердечники используют для точной настройки индуктивности или подстройки в небольших пределах, также длинные стержневые сердечники используют в магнитных антеннах радиоприёмников на средне- и длинноволновом диапазоне. Их объединяет то, что катушка индуктивности зачастую расположена не на средине сердечника. Ниже представлена катушка индуктивности на разомкнутом сердечнике, используемая в качестве магнитной антенны
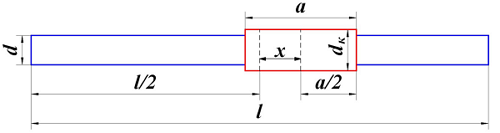
Расположение катушки индуктивности на сердечнике в магнитной антенне.
Как я уже говорил, размагничивающий фактор не равномерно распределён по длине разомкнутого сердечника. Его значение увеличивается от середины сердечника к его краям, а магнитная проницаемость, а соответственно уменьшается от центра сердечника к его краям. Чтобы не усложнять выражение для размагничивающего фактора введем корректирующий коэффициент pl, зависящий от расположения катушки на сердечнике
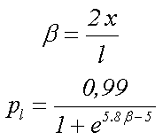
где х – расстояние от середины сердечника до середины катушки,
l – длина сердечника,
β – коэффициент, зависящий от расположения катушки на сердечнике.
Влияние размеров катушки относительно размеров сердечника
Как я писал выше, размагничивающий фактор неравномерен по длине сердечника, то необходимо учитывать любое различие в относительных размерах катушки индуктивности и сердечника.
Ещё одним существенным фактором при расчёте индуктивности является различие в длине катушки и длине сердечнике. Данное различие можно описать коэффициентом k, зависящем от отношения длины сердечника к длине катушки
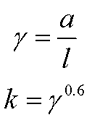
где а – длина катушки индуктивности,
l – длина сердечника,
γ – коэффициент, зависящий от отношения длины катушки к длине сердечника.
Пример расчёта индуктивности катушки на разомкнутом сердечнике
В качестве примера рассчитаем катушку индуктивности на разомкнутом сердечнике круглого сечения со следующими параметрами: диаметр сердечника dc = 6 мм, длина сердечника lc = 30 мм, катушка состоит из 30 витков провода диаметром dp = 1 мм, намотанных плотно виток к витку в один ряд, магнитная проницаемость материала сердечника μr = 600.
1.Рассчитаем индуктивность катушки без сердечника. Так как катушка намотана в один ряд, то для упрощения вычислений мы будем рассчитывать её как соленоид. Длина катушки составит lk = 30*1 = 30 мм, а диаметр катушки dk = dcp = 30,5 мм.
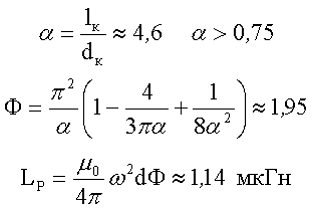
2.Вычислим эффективную магнитную проницаемость сердечника
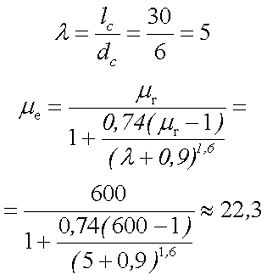
3.Рассчитаем поправочные коэффициенты на длину катушки и на расположении на сердечнике. Так как длина катушки совпадает с длинной сердечника и смещение катушки относительно сердечника отсутствует, то поправочные коэффициенты будут равны 1, тогда индуктивность данной катушки составит
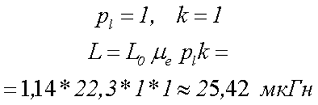
В качестве второго примера рассчитаем индуктивность магнитной антенны выполненной на сердечнике из феррита марки 600НН, размерами lc = 160 мм, dс = 8 мм, количество витков провода w = 60, диаметр провода dр = 0,15 мм. Катушка смещена на 30 мм относительно середины сердечника.
1.Рассчитаем индуктивность катушки без сердечника. Так как катушка намотана в один ряд, то для упрощения вычислений мы будем рассчитывать её как соленоид. Длина катушки составит lk = 60*0,15 = 9 мм, а диаметр катушки dk = dcp = 8,075 мм.
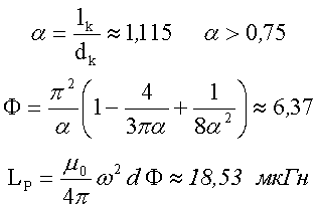
2.Вычислим эффективную магнитную проницаемость сердечника
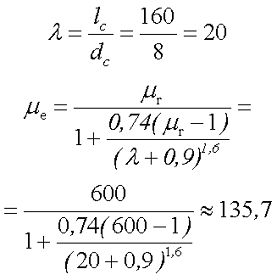
3.Рассчитаем поправочные коэффициенты на длину катушки и на расположении на сердечнике. Коэффициент, учитывающий расположение катушки на сердечнике составит
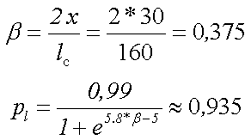
Коэффициент, учитывающий отношение длины катушки по отношению к длине сердечника составит
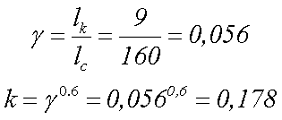
4.Рассчитаем индуктивность катушки индуктивности на разомкнутом сердечнике
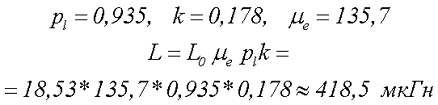
Данная статья заканчивает цикл расчётов индуктивности катушек с различными конструктивными параметрами.
Теория это хорошо, но необходимо отрабатывать это всё практически ПОПРОБОВАТЬ МОЖНО ЗДЕСЬ

 Катушки индуктивности с малым воздушным зазором
Катушки индуктивности с малым воздушным зазором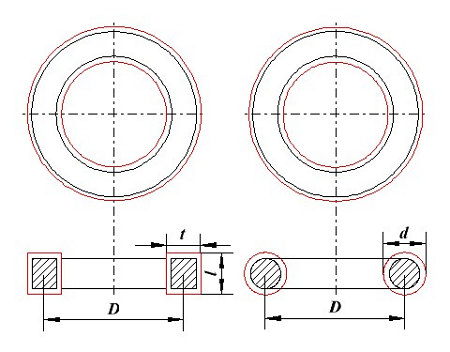 Расчёт индуктивности. Часть 3
Расчёт индуктивности. Часть 3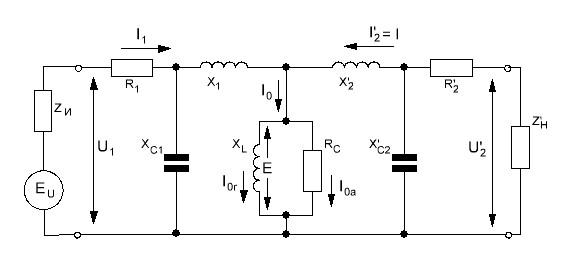 Эквивалентная схема трансформатора
Эквивалентная схема трансформатора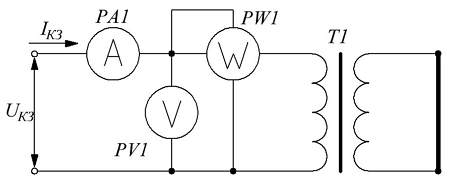 Режимы работы трансформатора. Часть 2
Режимы работы трансформатора. Часть 2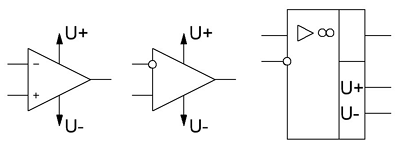 Операционные усилители. Начало
Операционные усилители. Начало