Всем доброго времени суток! В прошлой статье я рассказал о переменном напряжении и его параметрах. Данная статья, по сути, является продолжение предыдущей и затронет вопросы цепей переменного напряжения и тока, а также их воздействие на сопротивление, ёмкость и индуктивность в различных сочетаниях. Начнём с простейших цепей с синусоидальным переменным напряжением
Для сборки радиоэлектронного устройства можно преобрески DIY KIT набор по ссылке.
Сопротивление в цепи при переменном напряжении
Цепи переменного напряжения с сопротивлением является самыми простыми и наиболее часто встречающимися, поэтому начнём с них.
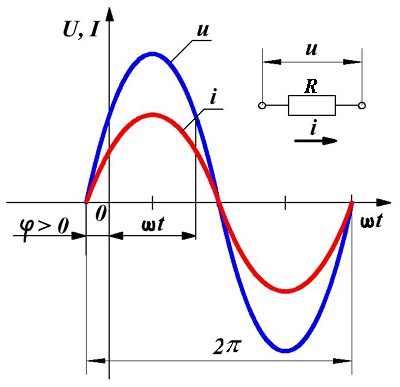
Переменное синусоидальное напряжение и ток в сопротивлении.
Допустим, что на сопротивление R подали переменное напряжение u, тогда, согласно с законом Ома, через данное сопротивление потечёт электрический ток i
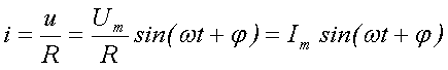
где Um – амплитудное значение переменного напряжения,
Im – амплитудное значение переменного тока,
ω – угловая частота,
t – время,
φ – начальная фаза
Таким образом, действующее I и среднее значение Icp переменного тока будут определяться следующими выражениями
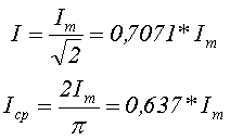
Так как, напряжение и ток, в цепи с сопротивлением имеют одинаковую начальную фазу, то есть, происходит совпадение фаз и достижение амплитудных значений напряжения Um и тока Im происходит одновременно.
Выражение «совпадение фаз» связанно с понятием фазового сдвига ψ, которое определяет разность начальных фаз двух синусоид одинаковой частоты. Следовательно, фазовый сдвиг между напряжением и током при активном сопротивлении будет равен нулю
![]()
где φu – начальная фаза напряжения,
φi – начальная фаза тока.
Для оценки энергетических характеристик ввели понятие мощности, в цепях переменного напряжения существует несколько мощностных характеристик. Одной из них является мгновенная мощность Рm, определяемая, как произведение мгновенных значений напряжения и тока
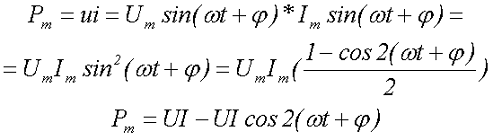
где Um – амплитудное значение переменного напряжения,
Im – амплитудное значение переменного тока,
U – действующее значение переменного напряжения,
I – действующее значение переменного тока.
Таким образом, мгновенная мощность Рm изменяется с удвоенной частотой по сравнению с частотой напряжения и тока и колеблется в пределах от 0 до 2UI.
Еще одной энергетической характеристикой является среднее значение мощности за период Р или активная мощность, которая определяется следующим выражением
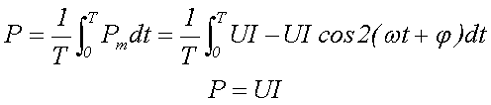
где Рm – мгновенная мощность,
U – действующее значение переменного напряжения,
I – действующее значение переменного тока.
Индуктивность в цепи при переменном напряжении
Следующий элемент, который я рассмотрю, будет индуктивный элемент, характеризующийся тем, что в нём возникает ЭДС самоиндукции.
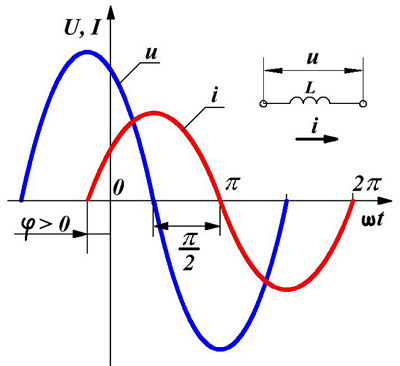
Переменное синусоидальное напряжение и ток в индуктивности.
При подаче переменного напряжения u на индуктивность L, в ней возникнет ЭДС самоиндукции
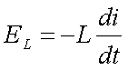
Тогда при условии, что сопротивление отсутствует R = 0, а разность потенциалов будет равна мгновенному значению напряжения u, получим
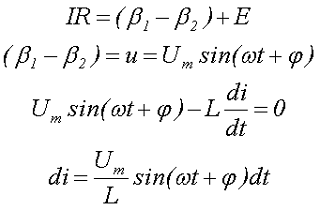
где (β1 – β2) – разность потенциалов,
Е – ЭДС самоиндукции,
Um – амплитудное значение переменного напряжения,
L – величина индуктивности,
ω – угловая частота,
t – время,
φ – начальная фаза
Тогда проинтегрировав получившееся выражение, получим значение мгновенного тока
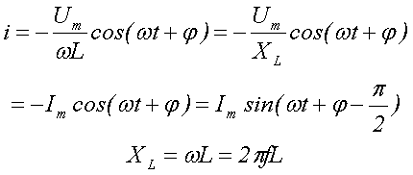
где Im – амплитудное значение переменного тока,
ω – угловая частота,
L – величина индуктивности,
f – частота переменного напряжения (тока),
XL – индуктивное сопротивление или реактивное сопротивление индуктивности.
Как видно из получившегося выражения ток i в индуктивности опаздывает от напряжения на угол π/2 или 90°. То есть фазовый сдвиг составит
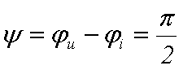
Оценим мгновенную мощность Pm в индуктивности при переменном напряжении
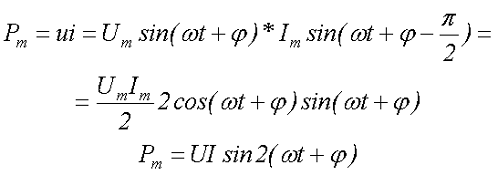
где Um – амплитудное значение переменного напряжения,
Im – амплитудное значение переменного тока,
U – действующее значение переменного напряжения,
I – действующее значение переменного тока.
Таким образом, мгновенная мощность колеблется с удвоенной частотой по сравнению с частотой напряжения (тока) и амплитудой UI.
Рассчитаем активную (среднее значение) мощность Р за период. Для этого необходимо проинтегрировать значение мгновенной мощности за весь период, а затем разделить на длительность периода
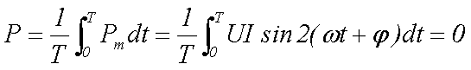
Как видно активная мощность на индуктивности не выделяется, то есть она затрачивается, но за счёт ЭДС самоиндукции происходит её компенсация.
Существенным параметром индуктивности при прохождении через неё переменного тока является энергия магнитного поля индуктивности WL, которая вычисляется по формуле
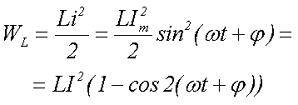
где Im – амплитудное значение переменного тока,
I – действующее значение переменного тока,
L – индуктивность.
Как видно из получившегося выражения, периодические изменения энергия магнитного поля происходят с удвоенной частотой по сравнению с частотой напряжения (тока) через катушку и значением от 0 до LI2.
Ёмкость в цепи при переменном напряжении
Третьим элементом, который я рассмотрю, будет емкость, которая характеризуется тем, что в ней происходит накопление электрической энергии.
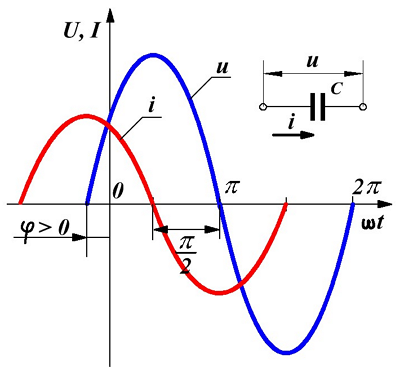
Переменное синусоидальное напряжение и ток в ёмкости.
Как известно напряжение на конденсаторе определяется по формуле
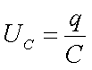
где q – величина заряда,
С – ёмкость конденсатора.
С учётом того что, вся ЭДС переменного напряжения Е = u приложена к конденсатору и сопротивление равно нулю R = 0, согласно закона Ома для полной цепи получим
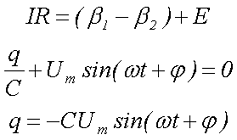
То есть величина заряда q будет изменяться пропорционально изменению напряжения u, а следовательно будет протекать электрический ток i.
Мгновенное значение электрического тока i при переменном напряжении на конденсаторе зависит от изменения электрического заряда dq за каждый период времени dt, тогда
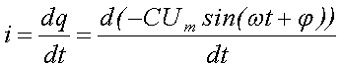
Проинтегрировав данное выражение получим
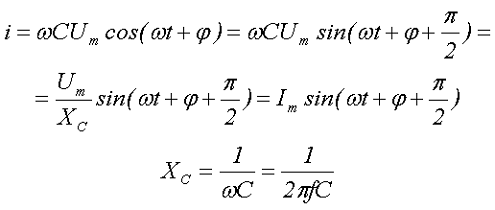
где Im – амплитудное значение переменного тока,
ω – угловая частота,
С – величина ёмкости,
f – частота переменного напряжения (тока),
XС – ёмкостное сопротивление или реактивное сопротивление ёмкости..
Фазовый сдвиг между напряжением и электрическим током в ёмкости при переменном напряжении составит
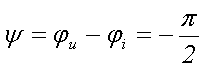
То есть напряжение в данном случае отстаёт от тока на 90°.
Определим энергетические характеристики в ёмкости. Мгновенное значение мощности Pm в ёмкости при переменном напряжении
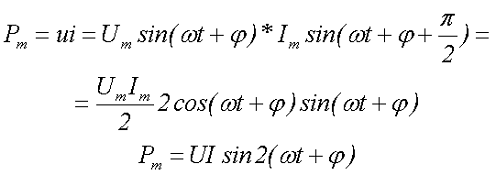
где Um – амплитудное значение переменного напряжения,
Im – амплитудное значение переменного тока,
U – действующее значение переменного напряжения,
I – действующее значение переменного тока.
Таким образом, значение мгновенной мощности в ёмкости аналогично значению мгновенной мощности в индуктивности, то есть колебания происходят с удвоенной частотой по сравнению с частотой напряжения (тока) и амплитудой UI.
В отличии от индуктивности, в ёмкости энергия запасённая в конденсаторе определяется напряжением
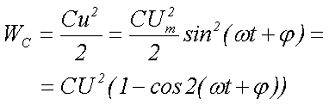
где Um – амплитудное значение переменного напряжения,
U – действующее значение переменного напряжения,
С – емкость.
Таким образом, энергия электрического поля в конденсаторе изменяется с удвоенной частотой по сравнению с частотой напряжения (тока) и может принимать значение от 0 до CU2.
На сегодня всё. В следующей статье я расскажу о параметрах различных соединений сопротивления, индуктивности и ёмкости при переменном напряжении и токе.
Теория это хорошо, но необходимо отрабатывать это всё практически ПОПРОБОВАТЬ МОЖНО ЗДЕСЬ

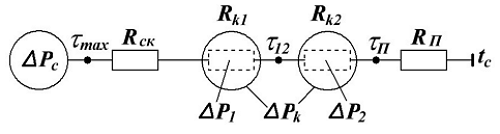 Тепловой режим трансформатора. Часть 2
Тепловой режим трансформатора. Часть 2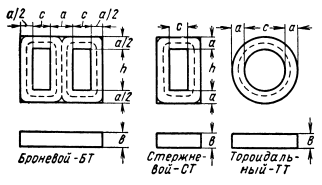 Классификация трансформаторов
Классификация трансформаторов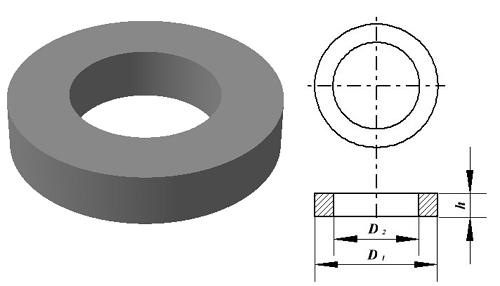 Как рассчитать индуктивность катушек с замкнутыми сердечниками?
Как рассчитать индуктивность катушек с замкнутыми сердечниками?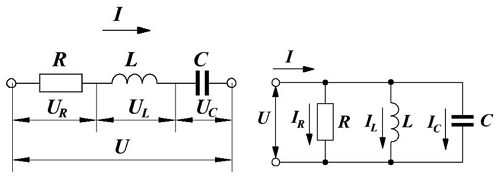 Соединение элементов в цепи переменного напряжения и тока
Соединение элементов в цепи переменного напряжения и тока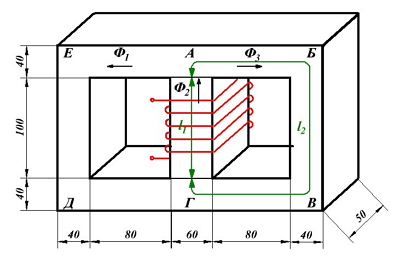 Магнитное поле в веществе. Часть 2
Магнитное поле в веществе. Часть 2