Всем доброго времени суток. В прошлых статьях я рассмотрел индуктивные элементы без сердечников, в частности, индуктивность прямого провода, индуктивность кольца и индуктивности различных типов круговых катушек. После этого можно было бы переходить к рассмотрению индуктивных элементов с сердечниками различной формы, однако существует ещё несколько типов катушек особой формы. Это, прежде всего, прямоугольные катушки и тороидальные катушки. Данная статья посвящена расчётам индуктивностей именно таких катушек.
Для сборки радиоэлектронного устройства можно преобрески DIY KIT набор по ссылке.
Прямоугольные катушки индуктивности
Прямоугольные катушки индуктивности, как видно из их названия, в поперечном разрезе имеют сечение прямоугольника (в отличии от круговых, где поперечный разрез имеет вид круга)
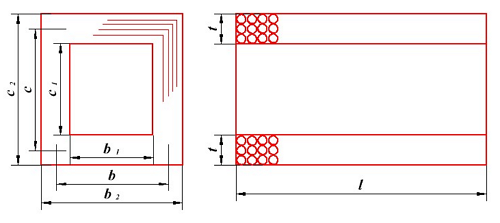
Поперечный (слева) и продольный (справа) разрез прямоугольной катушки индуктивности.
Данная катушка индуктивности имеет следующие конструктивные параметры:
c1b1 – размеры сердечника катушки (внутренние размеры обмотки);
c2b2 –внешние размеры катушки;
cb – средние размеры катушки;
l – длина катушки (аксиальный размер);
t – толщина намотки катушки (радиальный размер).
Для упрощение расчётов индуктивности, основными конструктивными параметрами прямоугольных катушек являются: средние размеры катушки c и b, толщина намотки t, длина катушки l. Средние размеры катушки вычисляются по следующим выражениям
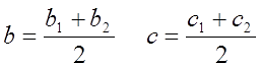
При расчётах предполагается, что толщина намотки t одинакова по всем сторонам катушки.
Прямоугольные катушки в зависимости от их длины и толщины намотки подразделяются также как и любые другие типы катушек (по аналогии с круговыми катушками):
длинная катушки, если длина катушки больше средних размеров (l > c, l > b);
короткая катушка, если длина катушки меньше средних размеров (l < c или l < b);
очень короткая катушка, если длина катушки намного меньше средних размеров (l << c или l << b);
плоская катушка, если принять длину намотки равной нулю (l = 0);
толстая катушка, если толщина намотки немного меньше или приблизительно равна средним размерам катушки (t ≈ c, t ≈ b);
тонкая катушка, если толщина намотки меньше средних размеров катушки (t < c, t < b);
соленоид, если толщина намотки принята равной нулю (t = 0).
Особенности расчёта прямоугольных катушек индуктивности
На индуктивность квадратных катушек, также как и на любой другой индуктивный элемент влияют конструктивные размеры катушки (длина, ширина, высота, толщина намотки) и размеры и форма проводников, из которых намотана катушка. Поэтому для квадратных катушек вводятся поправки на собственную индуктивность витков катушки ∆1L и взаимную индуктивность между витками катушки ∆2L, которые вычисляются по аналогии с круговыми катушками
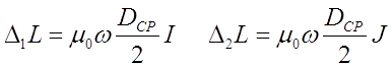
где
μ0 – магнитная постоянная, μ0 = 4π•10-7 Гн/м;
ω – число витков соленоида;
DСР – средний диаметр катушки, м;
I и J – коэффициенты, зависящие от расположения и от числа витков катушки.
А полная индуктивность катушки составит
![]()
где LР – расчётная индуктивность;
∆L – поправка на «изоляцию», ∆L = ∆1L + ∆2L;
∆1L – поправка учитывающая влияние индуктивности витков;
∆2L – поправка учитывающая влияние взаимной индуктивности витков.
Длина намотки l и толщина намотки t принимается равными шагу обмотки (p – шаг по длине катушки, q – шаг по толщине намотки) умноженному на количество слоёв в том или ином направлении ω
![]()
Если у катушки в каком-либо направлении (по длине намотки l или по толщине намотки t) имеется только один ряд (или слой), то в этом направлении размер l или t можно принять равным нулю, то есть расчёт ведётся как для соленоида или плоской катушки.
В некоторых случаях, при большом диаметре провода или шаге намотки у однослойных катушках размер l или t принимается равным диаметру голого провода d.
Так как величина поправки на взаимную индуктивность ∆2L в несколько раз меньше, чем поправка на индуктивность витков ∆1L, то при расчётах можно учитывать только ∆1L.
Индуктивность квадратного соленоида
В начале, рассмотрим простейший вариант прямоугольной катушки – квадратный соленоид, в которой средние размеры катушки равны между собой c = b
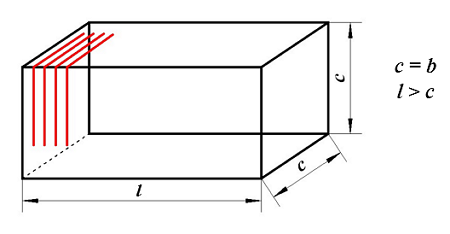
Расчёт квадратного соленоида.
Как известно соленоид представляет собой катушку, толщина которой бесконечно мала или равна нулю (t = 0) выражение для расчёта индуктивности такой катушки будет иметь вид
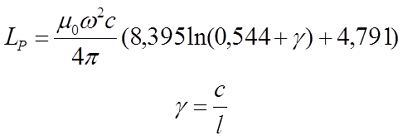
где μ0 – магнитная постоянная, μ0 = 4π•10-7 Гн/м;
ω – число витков соленоида;
с – сторона квадрата, являющегося основанием соленоида;
γ – величина зависящая от отношения стороны основания и длины намотки;
l – длина намотки соленоида.
Пример. В качестве примера рассчитаем квадратный соленоид длиной l = 5 см = 0,05 м, стороной основания с = 0,5 см = 0,005 м и числом витков ω = 100.
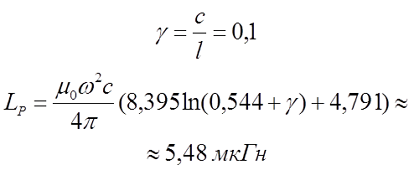
Вышеописанное выражение для индуктивности квадратного соленоида возможно использовать и для вычисления большинства однослойных катушек прямоугольного сечения с учётом поправок на изоляцию из в предыдущей статьи.
Индуктивность прямоугольного соленоида
Следующим типом катушки будет прямоугольный соленоид представленный ниже
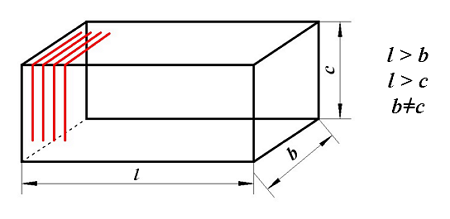
Расчёт прямоугольного соленоида.
В отличие от квадратного соленоида, в котором стороны основания равны (c = b), в прямоугольном соленоиде стороны основания не равны (c ≠ b). В данном случае выражение для индуктивности такого соленоида несколько сложнее и зависит от соотношения сторон основания между собой и к длине соленоида
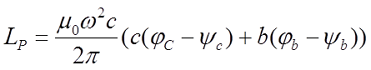
где μ0 – магнитная постоянная, μ0 = 4π•10-7 Гн/м;
ω – число витков соленоида;
с, b – сторона квадрата, являющегося основанием соленоида;
φb, φс, ψb, ψc – величины зависящие от соотношения сторон между собой и к длине соленоида.
Коэффициенты φb, φс зависят от γb и γс соответственно
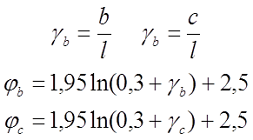
где c и b – размеры основания соленоида;
l – длина катушки (аксиальный размер);
Коэффициенты ψb, ψс зависят от δb, δс
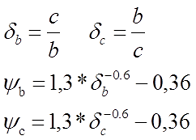
где c и b – размеры основания соленоида;
Пример. В качестве примера рассчитаем индуктивность прямоугольного соленоида длиной l = 7 см = 0,07 м, размерами основания с = 2 см = 0,02 м, b = 4 см = 0,04 м и числом витков ω = 400.
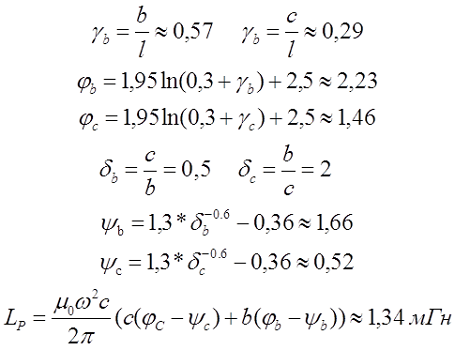
Индуктивность квадратной плоской катушки
Теперь рассмотрим квадратную плоскую катушку средними размерами основания с и толщиной намотки t
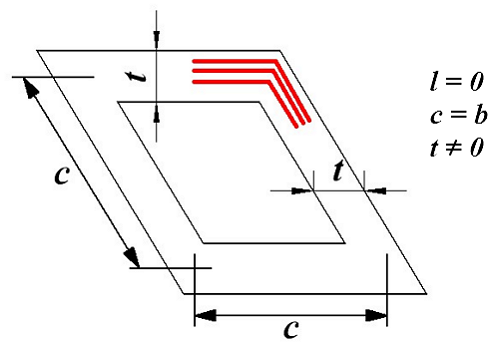
Расчёт индуктивности квадратной плоской катушки.
В данном случае длину катушки можно принять равной нулю (l = 0), а стороны основания равны между собой (c = b). Тогда индуктивность такой катушки можно найти по следующему выражению
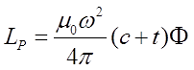
где μ0 – магнитная постоянная, μ0 = 4π•10-7 Гн/м;
ω – число витков плоской катушки;
с – сторона квадрата, являющегося основанием плоской квадратной катушки;
Φ – коэффициент зависящий от размеров катушки и толщины намотки.
Величину Φ зависящую от соотношения средней длины основания c и толщины намотки катушки t можно оценить по следующему выражению
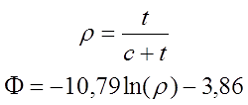
где t – толщина намотки катушки,
с – размер основания катушки.
Пример. Рассчитаем плоскую прямоугольную катушку со средней длиной стороны с = 50 см = 0,5 м, толщиной намотки t = 5 см = 0,05 м и имеющая ω = 100 витков.
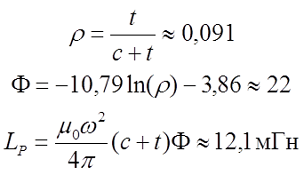
Индуктивность прямоугольной катушки прямоугольного сечения
Отдельно необходимо рассмотреть прямоугольную катушку прямоугольного сечения, в которой длина l и толщина t намотки значительно меньше, чем средние размеры её сторон b и c.
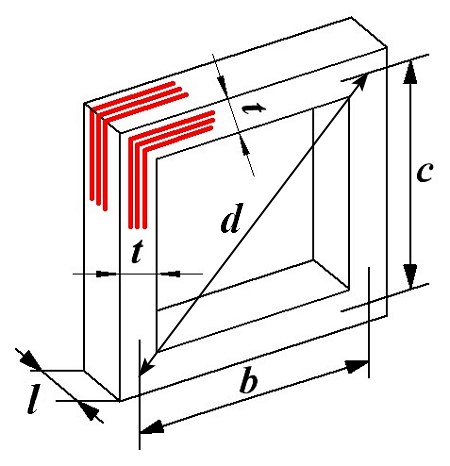
Расчёт индуктивности прямоугольной катушки прямоугольного сечения.
Индуктивность такой катушки можно вычислить достаточно точно по следующему выражению
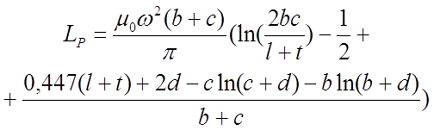
где μ0 – магнитная постоянная, μ0 = 4π•10-7 Гн/м;
ω – число витков катушки;
с,b – средние длины сторон основания прямоугольной катушки;
d – диагональ основания катушки;
t – толщина намотки катушки;
l – длина катушки.
![]()
В случае равенства сторон основания (c = b), то есть квадратной катушки, то выражение приобретает вид
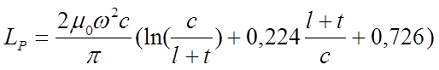
где μ0 – магнитная постоянная, μ0 = 4π•10-7 Гн/м;
ω – число витков катушки;
с – средняя длинна стороны основания катушки;
d – диагональ основания катушки;
t – толщина намотки катушки;
l – длина катушки.
Индуктивность тороидальных катушек
Заканчивая рассмотрение расчётов индуктивностей катушек без сердечников, остановлюсь на таких распространённых индуктивных элементах, как тороидальные катушки. Они имеют ряд преимуществ перед предыдущими индуктивными элементами, в частности, лучшие массогабаритные показатели.
Рассмотрим два типа катушек: прямоугольным сечением и с круговым сечением каркаса
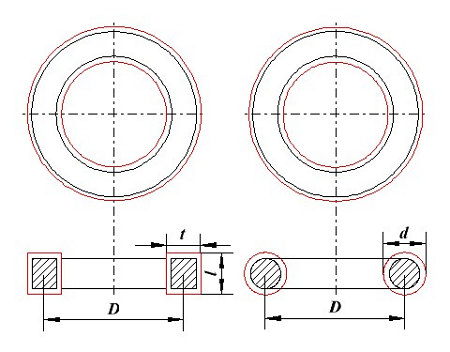
Тороидальные катушки: с прямоугольным сечением каркаса (слева) и круговым сечением каркаса (справа).
Индуктивность тороидальной катушки с прямоугольным сечением каркаса определяется по следующей формуле
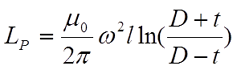
где μ0 – магнитная постоянная, μ0 = 4π•10-7 Гн/м;
ω – число витков катушки;
t – толщина катушки;
l – высота катушки;
D – средний диаметр катушки.
Индуктивность тороидальной катушки с круговым сечением каркаса можно вычислить по следующему выражению
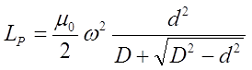
где μ0 – магнитная постоянная, μ0 = 4π•10-7 Гн/м;
ω – число витков катушки;
D – средний диаметр катушки;
d – средний диаметр обмотки.
На этом закончу рассмотрение выражений для расчёта индуктивностей элементов без сердечников. В следующей статье я буду рассматривать влияние различных типов сердечников на индуктивность элементов.
Теория это хорошо, но необходимо отрабатывать это всё практически ПОПРОБОВАТЬ МОЖНО ЗДЕСЬ

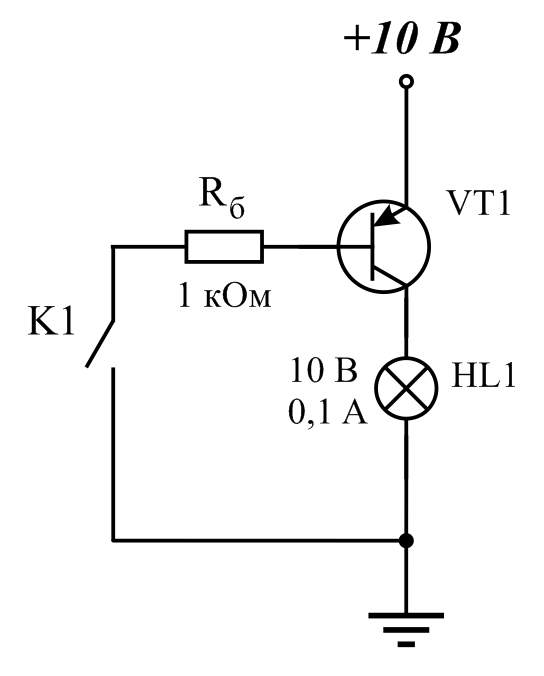 Биполярные транзисторы.Часть 2. Ключевой каскад.
Биполярные транзисторы.Часть 2. Ключевой каскад.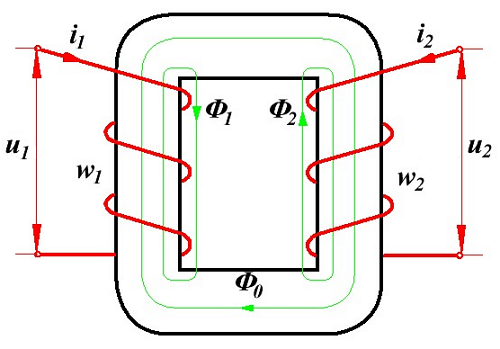 Устройство и схема трансформатора
Устройство и схема трансформатора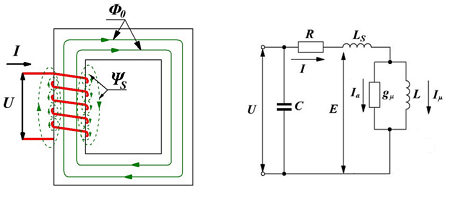 Дроссель и его параметры
Дроссель и его параметры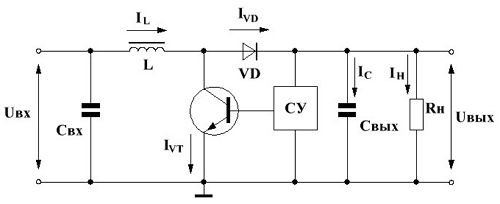 Повышающий преобразователь напряжения
Повышающий преобразователь напряжения