Всем доброго времени суток! В прошлой статье я рассказывал о таком явлении как электромагнитная индукция и ЭДС возникающая при самоиндукции и взаимной индукции. Устройства, в основе которых лежат данные явления и процессы, называются индуктивными элементами (катушки колебательных контуров, трансформаторы, дроссели, реакторы). В качестве одного из основных параметров данных элементов выступает индуктивность L(также имеет название коэффициента самоиндукции). О том, как рассчитать данный параметр пойдёт речь в данной статье.
Для сборки радиоэлектронного устройства можно преобрески DIY KIT набор по ссылке.
Методы расчёта индуктивностей
Индуктивностью (обозначается L) или коэффициентом самоиндукции называется коэффициент пропорциональности между потокосцеплением (обозначается ΨL) и электрическим током, который возбуждает данное потокосцепление.
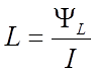
В простых случаях индуктивность можно рассчитать, применяя формулы для вычисления магнитной индукции B0 (закон Био-Савара-Лапласа), магнитного потока Φ и потокосцепления ΨL
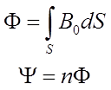
где S – площадь поверхности ограниченная контуром, который создает магнитную индукцию;
n – количество контуров с током, которые пронизывает магнитный поток.
Однако это в идеальном случае, в реальности говоря о токе I, который протекает по проводнику, необходимо отметить, что его распределение по сечению проводника не всегда равномерно, вследствие возникновения скин-эффекта при переменном токе. В результате этого эффекта плотность электрического тока распределяется неравномерно, происходит её уменьшение от внешнего слоя проводника к его центру. Уменьшение плотности тока также происходит неравномерно и зависит от частоты переменного тока. Для оценки скин-эффекта ввели понятие толщины скин-слоя ∆, которая показывает, на каком расстоянии от поверхности проводника плотность тока падает в е = 2,718 раз. Толщину скин-слоя можно вычислить по выражению
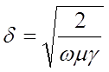
где δ – глубина проникновения переменного тока или толщина скин-слоя;
μ – магнитная проницаемость вещества;
γ – удельная электрическая проводимость материала проводника;
ω – круговая частота переменного тока, ω = 2πf.
Поэтому непосредственный способ вычисления индуктивности практически не применяется.
На практике применяется выражения для индуктивности, выведенные с некоторыми допущениями, погрешности вычисления индуктивности по этим выражениями составляет порядка нескольких процентов.
Так как индуктивные элементы довольно разнообразны, их можно разделить на три группы:
индуктивные элементы без сердечников;
индуктивные элементы с замкнутыми сердечниками;
индуктивные элементы с сердечниками, имеющие воздушный зазор.
Самые простые по конструкции являются индуктивные элементы без сердечников, поэтому рассмотрим их в первую очередь. Простейшим из таких элементов является прямой провод.
Индуктивность прямолинейного провода круглого сечения
При расчёте индуктивности необходимо разделять индуктивность на постоянном токе и индуктивность на высокой частоте. Под высокой частотой следует понимать такую частоту, на которой толщина скин-слоя меньше размеров поперечного сечения провода. В случае если толщина скин-слоя больше поперечных размеров провода, то можно вести расчёт для постоянного тока.
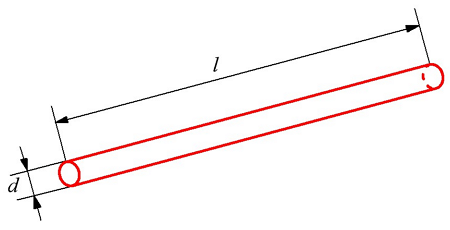
Определение индуктивности прямого провода. l – это длина проводника, d = 2r – диаметр проводника.
В случае постоянного тока или тока низкой частоты индуктивность составит
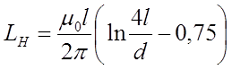
где μ0 – магнитная постоянная, μ0 = 4π•10-7 Гн/м;
l – длина провода, м;
d – диаметр провода, м.
Как я уже говорил, на величину индуктивности влияет частота переменного тока, поэтому в случае необходимости рассчитать индуктивность на любой частоте применяется следующее выражение
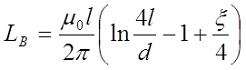
где ξ – коэффициент, вносящий поправку на распространение переменного тока по сечению провода. Данный коэффициент зависит от величины k*r, где
d = 2r – диаметр поперечного сечения провода, м.
![]()
где ω – угловая частота переменного тока, ω = 2πf;
μ0 – магнитная постоянная, μ0 = 4π•10-7 Гн/м;
γ – удельная проводимость вещества проводника.
Тогда если k*r < 3, то
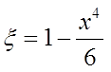
если k*r > 3, то
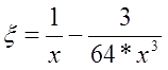
где
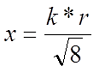
Пример. Необходимо рассчитать индуктивность прямолинейного провода круглого сечения из меди (γ = 5,81*107 См/м) диаметром d = 2 мм и длиной l = 4 м, при постоянном токе и токе частотой f = 50 кГц.
На постоянном токе
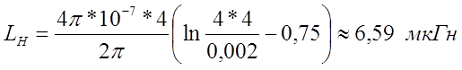
На частоте 50 кГц
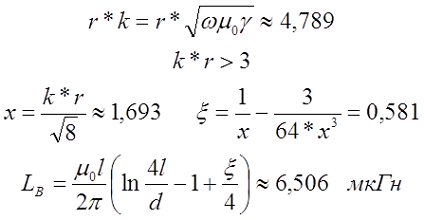
Online калькулятор индуктивности прямолинейного проводника
Индуктивность кругового кольца круглого сечения
Теперь рассмотрим, какова будет индуктивность если провод свернуть в кольцо. Такой индуктивный элемент будет иметь вид
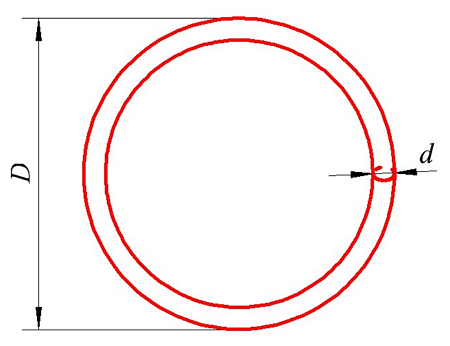
Определение индуктивности кругового витка. D – диаметр кольца (витка), d – диаметр провода, из которого сделано кольцо (виток).
При этом его индуктивность можно вычислить по следующему выражению
для постоянного тока
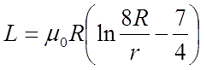
где R – радиус витка, м, R = D/2;
r – радиус провода, м, r = d/2;
μ0 – магнитная постоянная, μ0 = 4π•10-7 Гн/м.
Так же как и для проводника существует выражение для индуктивности кругового витка на любой частоте
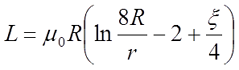
где ξ – коэффициент, вносящий поправку на распространение переменного тока по сечению провода. Определяется также как и для прямого проводника.
Пример. В качестве примера рассчитаем индуктивность такого же провода, как и в первом примере, только свёрнутом в кольцо. В этом случае диаметр провода d = 2 мм, а диаметр кольца D = l/π = 4/3,142 ≈ 1,273 м, провод выполнен из меди (γ = 5,81*107 См/м).
Для постоянного тока индуктивность составит
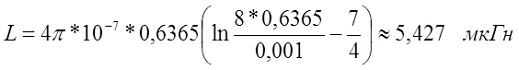
На частоте 50 кГц
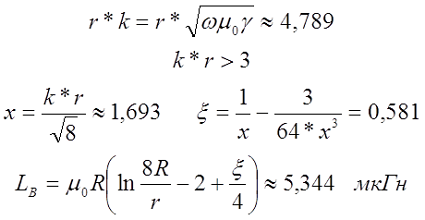
Online калькулятор индуктивности кольца кругового сечения
В следующей части я продолжу рассмотрение расчётов индуктивности для различных индуктивных элементов.
Теория это хорошо, но необходимо отрабатывать это всё практически ПОПРОБОВАТЬ МОЖНО ЗДЕСЬ

 Основы электротехники. Часть 1 электростатика
Основы электротехники. Часть 1 электростатика Как рассчитать индуктивность катушек с замкнутыми сердечниками? Часть 2.
Как рассчитать индуктивность катушек с замкнутыми сердечниками? Часть 2. Как рассчитать индуктивность катушек с замкнутыми сердечниками?
Как рассчитать индуктивность катушек с замкнутыми сердечниками?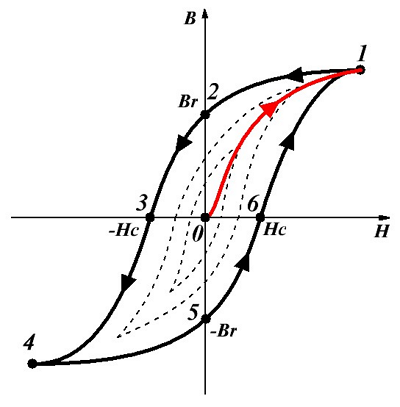 Магнитное поле в веществе. Часть 1
Магнитное поле в веществе. Часть 1